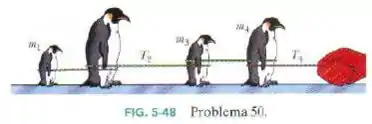
A Fig. 5-48 mostra quatro pinguins que estão sendo puxados sobre o gelo muito escorregadio (sem atrito) por um zelador. As massas de três pinguins e a tensão em duas das cordas são e . Determine a massa do pinguim , que não é dada.
Passo 1
Vamos primeiramente juntar os dados que temos:
- Algumas das forças aplicadas em cada pinguim;
- Massas dos pinguins (exceto um).
E agora as informações que concluímos do problema:
- As cordas são inextensíveis, portanto, o deslocamento dos pinguins devem ser iguais;
- Deslocamentos iguais implicam em acelerações iguais;
- Os pinguins se movimentam somente na horizontal.
Temos então relação entre forças, massas e aceleração, podemos usar a segunda lei de Newton no diagrama de corpo livre de cada pinguim. Nos próximos passos os pinguins se tornarão, como qualquer coisa na Dinâmica, blocos. Como só vamos analisar o movimento horizontal, incluiremos no diagrama somente as forças horizontais.
Passo 2
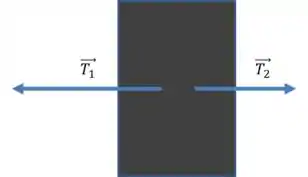
No pinguim de massa :
Usando a segunda lei:
Substituindo os valores de e :
(Eq. 1)
Passo 3
No pinguim de massa :
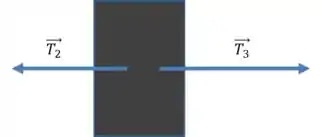
Usando a segunda lei:
Substituindo os valores de e :
(Eq. 2)
Passo 4
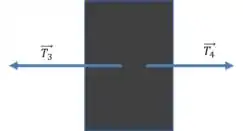
No pinguim de massa :
Usando a segunda lei:
Substituindo os valores de :
(Eq. 3)
Passo 5
No pinguim de massa :
Usando a segunda lei:
Substituindo os valores de :
(Eq. 4)
Passo 6
Somando todas as equações, de 1 a 4, obtemos:
(Eq.5)
OBS.: A equação acima mostra como podemos encarar o conjunto de pinguins como um único corpo. A única força externa do sistema é .
Deixa esse resultado guardado por um segundo.
Agora, observando bem as equações podemos ver que se somarmos as Eqs 1 e 2 teremos como achar a aceleração:
Substituindo na Eq. 5, temos: