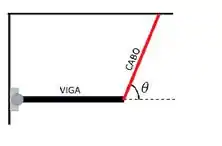
A figura ao lado ilustra uma viga homogênea de peso P. A viga está sustentada na posição horizontal por uma dobradiça e por um cabo, que forma um ângulo em relação à direção da viga, como ilustrado ao lado. Quais são o módulo e o sentido da força horizontal que a dobradiça exerce sobre a viga?
a)
b)
c)
d)
e)
f)
g)
h)
i) 0
Passo 1
Dá uma olhada nessa decomposição de forças que eu fiz aqui:
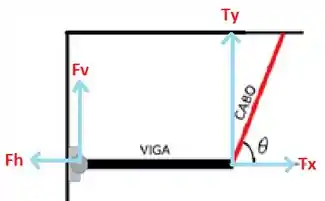
Chamando a tensão na corda de T, nós vamos ter:
E ainda teremos o peso ali no centro de massa da barra.
O equilíbrio de forças verticais vai ficar:
E o equilíbrio de forças horizontais:
Ali na decomposição das forças já te dei spoiler da orientação de né, que é o que queremos descobrir. Já sabemos então que é para a esquerda, vamos descobrir o módulo dela agora.
Passo 2
Ó, eu vou fazer o somatório dos momentos com relação à extremidade direita da barra. Isso vai me dar mais uma equação pra ajudar a resolver o problema:
Show! Agora vamos substituir:
Agora vamos voltar laaaaa em Fh:
E pra esquerda, então a setinha tem que tá assim:
Resposta
Letra H.