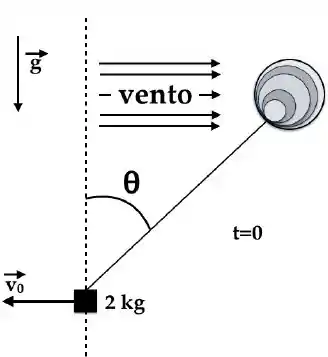
Um balão está preso a um bloco por meio de um fio ideal (massa desprezível e inextensível). A massa do bloco é de . A tensão (módulo) no fio entre o bloco e o balão é de de 30N. O ventor arrasta o balão de modo que o fio faz um ângulo em relação a vertical (ver figura abaixo). Assuma que o módulo da aceleração da gravidade local é . Assuma ainda que o bloco é pequeno, de maneira que a força do vento sobre o bloco é desprezível. A figura mostra o vetor velocidade inicial do bloco cujo módulo é de.

Passo 1
. letra a)
Pra fazer o diagrama de forças vamos adotar os eixos e e tradicionais, ou seja, a gravida ficará apontando para baixo:
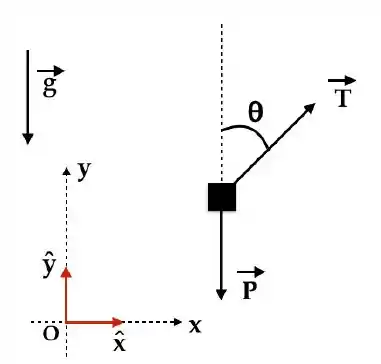
A força tração é feita pelo fio que sustenta o bloco e a força peso é feito pelo campo gravitacional.
Passo 2
Letra b)
Pela segunda Lei de Newton, temos que a resultante das forças é o produto da massa e aceleração, sendo assim, vamos decompor as forças nos eixos que usamos e aplicar a lei.
Eixo x:
Eixo y:
Sendo assim, montamos a expressão vetorial da aceleração:
Passo 3
Letra c)
Agora vamos separar a expressão em dois eixos e no final a gente junta tudo, ok?
Sabemos que a expressão em cada eixo tem que ficar assim
Para o
Para o temos:
Para o temos:
Juntando as expressões de cada eixo ficamos
Logo:
Passo 4
Letra d)
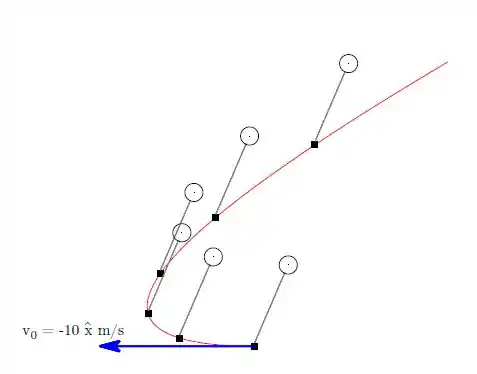
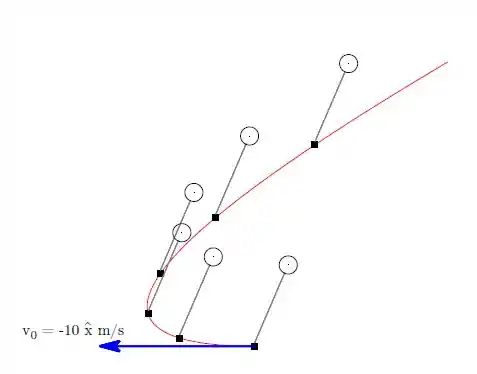
Como a aceleração do bloco no eixo é positiva e não há nenhuma velocidade no sentido contrário, o balão irá subir sempre. Já no eixo como a velocidade inicial é negativa, ela irá primeiramente para a esquerda e depois de um certo tempo irá voltar para o eixo positivo, fazendo o movimento de uma parábola.
Passo 5
Se o balão tem massa desprezível, temos que pela segunda Lei de Newton a soma de forças tem que ser .
Como queremos a força do vento, temos que no eixo a resultante tem que ser .
Como já sabemos o valor de , é só substituir na nossa equação e pela terceira lei de Newton temos que , porque agora estamos trabalhando com o balão!!!
Resposta
a)
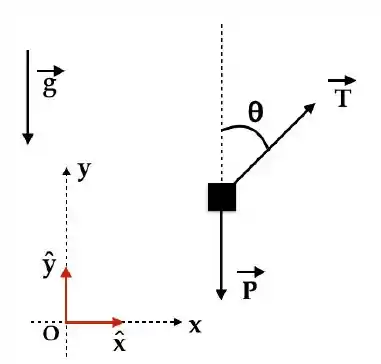
b)
c)
d)
e)