UFPB, Sem Campus, Física Geral II, P1 - 2021.2, Questão 2.
2) A figura mostra uma barra de de comprimento e massa desprezível, suspensa por uma corda , sustentando um peso de no ponto indicado. Sabendo que a barra se apoia sem atrito nas paredes do vão, qual a razão entre a tensão na corda e a reação na parede no ponto , no equilíbrio estático?
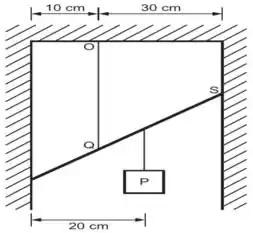
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nosso objetivo nesse problema é calcular a razão entre a tensão na corda e a força na parede no ponto .
E aí, parece complicadinho, não é?
Um sistema de forças em equilíbrio ocorre quando a soma vetorial das forças que atuam sobre um objeto é igual a zero, o que significa que as forças estão equilibradas e o objeto não está acelerando.
Para resolver um sistema de forças em equilíbrio, é necessário seguir alguns passos:
Primeiro: Desenhe um diagrama de corpo livre.
Segundo: Identifique todas as forças.
Terceiro: Decomponha as forças em componentes.
Quarto: Aplique as equações de equilíbrio. Existem duas equações de equilíbrio: a equação de equilíbrio em e a equação de equilíbrio em .
Por fim: Resolva as equações de equilíbrio.
Tranquilo? 😉
Passo 2
Primeiro vamos desenhar as forças presentes no sistema.
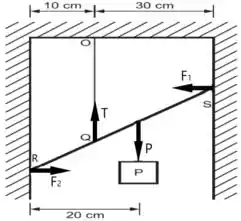
Se o sistema está estático e não há atrito entre a parede e a barra, as reações na parede serão perpendiculares a ela.
Dessa forma, se o sistema está em equilíbrio, a soma das forças em e a soma das forças em devem ser iguais a
Se no enunciado foi dito que o peso , então .
Porém para obter e é um pouco mais complicado...
Entendeu essa parte? 😉
Passo 3
Você concorda que a barra está fixa no ponto ? Portanto a barra tende a rotacionar no sentido horário pela ação do peso .
Escrevendo o momento rotacional usando como referência o ponto de contato temos que
O momento é a força multiplicado pela distância até o eixo de rotação, no caso, o ponto
A Tração faz a barra rotacionar no sentido anti-horário assim como a força , já a força faz a barra rotacionar no sentido horário, então a soma dos momentos pode ser escrita como
Como está na horizontal e a componente da força que gera a rotação deve estar na vertical, então temos que encontrar aplicando Pitágoras no desenho da barra...
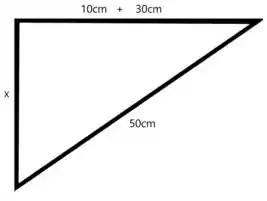
Assim, por sequência pitagórica, . Resultando em
Se , logo
Queremos a relação , ou seja
Fim! Iae, o que achou? Responde Aí! 😁
