UERJ, Sem Campus, Física I, Listas de F1 - Profª Fernanda Deus - Lista 5 - Força e Movimento I, Questão 18
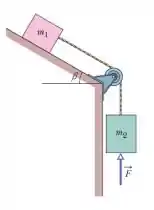
Na figura, uma lata de antioxidante sobre um plano inclinado sem atrito está ligada a uma lata de apresuntado . A polia tem massa e atrito desprezíveis. Uma força vertical para cima de módulo atua sobre a lata de apresuntado, que tem uma aceleração para baixo de Determine a tensão da corda e o ângulo .
Passo 1
Faaaala galera, tudo bem com vocês?
Nessa questão temos um arranjo de duas latinhas presas por um fio, que passa por uma poia, onde uma das latas está pendurada verticalmente, e outra está apoiada em um plano inclinado. Conforme mostrado na figura abaixo:
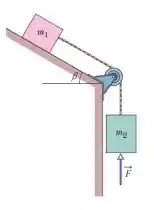
Sabemos que no bloco atua uma força , e que a aceleração dele é de .
(Mas, como o comprimento do fio é constante, a aceleração do bloco precisa valer a mesma coisa, beleza?!)
Queremos calcular a tração na corda bem como o ângulo do plano inclinado.
Para fazer isso vamos escrever a segunda lei de Newton para cada um dos blocos:
Onde:
é a força resultante;
é a massa do objeto;
é a aceleração do objeto;
Vamo nessa!
Passo 2
Começando pelo bloco , atuam nele a tração, a força peso, e a força para cima.
Logo:
Mas temos , , daí:
Portanto:
Muito bom!
Passo 3
Agora vamos escrever a equação da segunda lei de Newton para o bloco , que está apoiado no plano inclinado. A componente da força peso na direção do plano é um resultado bem conhecido, que vale a pena a gente guardar pra ganhar tempo nos exercícios:
Daí, atuam no bloco essa componente da força peso e a força de tração, ambas no mesmo sentido.
Substituindo os valores dados, temos:
Logo:
Daí:
É isso galera! Muito obrigado pela atenção de vocês!
Até a próxima 😉