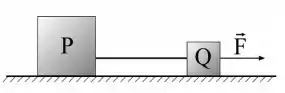
Dois corpos P e Q em uma superfície horizontal sem atrito estão ligados por uma corda de massa desprezível. A massa de P é maior do que a de Q. Uma força horizontal de módulo é aplicada sobre Q como mostrado na figura, acelerando os dois corpos para a direita. O módulo da tração exercida pela corda sobre P é:
(A) Zero.
(B) Maior do que zero, porém menor do que o módulo de F.
(C) Igual ao módulo de F.
(D) Maior do que o módulo de F.
(E) Menor do que o módulo da tração da corda sobre Q.
Passo 1
De uma maneira bemmmm simplista, a ideia é a seguinte:
A força está puxando os dois corpos, ou seja, está responsável por acelerar tanto a massa de Q, quanto a massa de P.
Já a força de tração sobre a corda está puxando apenas o corpo P, ou seja, essa força está sendo responsável por acelerar apenas a massa de P.
Assim, essa força de tração é menor que a força . Isso até que é coerente, considerando que a força de tração é uma consequência da aplicação da força .
Masss, vamos fazer as contas para confirmar essa ideia.
Passo 2
Para achar uma relação entre as forças e a de tração, vamos fazer o diagrama do corpo livre (D.C.L.) apenas no corpo Q (já é suficiente nesse caso) e aplicar a Segunda Lei de Newton.
Corpo Q:
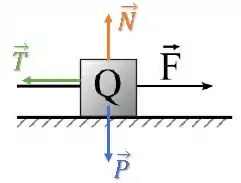
O corpo está acelerando para a direita, então, temos:
Isolando :
Ou seja, podemos ver que o módulo da força de tração (mesma sobre toda a corda) é igual ao módulo da força menos um termo que é positivo.
Assim, o módulo da força de tração é menor que o módulo da força :
Ficamos com a alternativa (B).
Resposta
Letra (B)