UERJ, Sem Campus, Física I, Listas de F1 - Profª Fernanda Deus - Lista 5 - Força e Movimento I, Questão 17
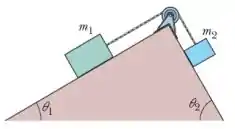
A figura mostra um bloco sobre um plano inclinado sem atrito de ângulo . O bloco está ligado por uma corda de massa desprezível a um outro bloco ( situado sobre um plano inclinado sem atrito de ângulo . A polia não tem atrito e a massa é desprezível. Qual é a tensão da corda?
Passo 1
E aí gente, tudo na paz com vocês?
Nessa questão temos um plano inclinado duplo haha, onde em cada lateral tem um bloco. Eles estão ligados por uma corda, que passa por uma polia. São dadas as massas do bloco, bem como o ângulo .
Queremos calcular justamente a tensão nessa corda.
Uma dificuldade desse problema é sabermos em qual eixo decompormos as forças atuantes nos bloquinhos. A dica é sempre procurar fazer essa decomposição no sentido tangencial ao movimento dos blocos. Nesse caso, para cada um dos blocos devemos decompor as forças no sentido do plano inclinado, beleza?
E, a partir disso, aplicamos a segunda lei de Newton para escrever a equação da força resultante.
Vamo nessa!
Passo 2
Gente, sempre que temos um plano inclinado e precisamos decompor as forças na direção do plano, uma decomposição super comum é a da força peso.
A componente da força peso na direção do plano, vale:
A única outra força que atua nos blocos na direção do plano é a tração na corda.
Como o bloco é o mais pesado, vamos supor que ele irá descer o plano, enquanto o bloco irá subir.
Além disso, foi dado apenas o ângulo , mas o plano é um triângulo retângulo na polia. Assim:
Prontinho! Assim, para o bloco , temos:
Já para o bloco , temos:
Somando as duas equações, temos:
Muito bom!
Passo 3
Pra calcular a tração na corda, basta substituirmos esse resultado na segunda lei de Newton:
Logo:
Ou, fazendo as contas:
Prontinho galera, obrigado pela atenção.