UFPB, Sem Campus, Física Geral II, P1 - 2021.2, Questão 1.
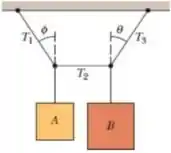
1) O sistema da Fig. abaixo está em equilíbrio, com a corda do centro exatamente na horizontal. O bloco pesa , o bloco pesa e o ângulo é . Determine (a) a tração , (b) a tração , (c) a tração e (d) o ângulo .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema, temos um sistema composto por dois blocos ( e ) que estão suspensos por três cordas, nessas cordas há tração e nosso objetivo é obter a tração , , e o ângulo da figura.
Tem ideia de como fazemos isso? 🤔
Um sistema de forças em equilíbrio ocorre quando a soma vetorial das forças que atuam sobre um objeto é igual a zero, o que significa que as forças estão equilibradas e o objeto não está acelerando.
Para resolver um sistema de forças em equilíbrio, é necessário seguir alguns passos:
Primeiro: Desenhe um diagrama de corpo livre.
Segundo: Identifique todas as forças.
Terceiro: Decomponha as forças em componentes.
Quarto: Aplique as equações de equilíbrio. Existem duas equações de equilíbrio: a equação de equilíbrio em x e a equação de equilíbrio em y.
Por fim: Resolva as equações de equilíbrio.
Tranquilo? 😉
Passo 2
Vamos começar com o nó ligado diretamente ao bloco . Nele temos
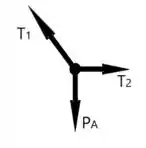
Decompondo em e em , vamos obter que
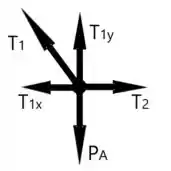
Se o sistema está em equilíbrio, então obrigatoriamente e
No enunciado foi dito que e o ângulo de com o eixo é . Portanto, podemos dizer que
Já temos e , então já podemos encontrar ...
Da mesma forma podemos dizer que
Já temos e temos , logo
Tranquilo até aqui? 😁
Passo 3
Agora vamos para o segundo nó do sistema... analisando as forças que agem sobre ele e fazendo a decomposição, temos
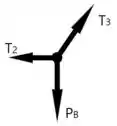
Perceba que e , logo, se o modulo de é dado por , então
Anteriormente calculamos que e no enunciado foi dado que , ou seja
Agora, fazendo as equações de equilíbrio em e nesse ponto, temos
Usando uma dessas equações, podemos obter o ângulo
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
a)
b)
c)
d)