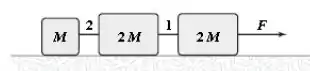
Os três blocos da figura abaixo deslizam sobre a superfície horizontal sem atrito. Se a tensão na corda 1 é de , determine o módulo de .
A)
B)
C)
D)
E)
Passo 1
Para descobrirmos o módulo de , precisamos aplicar a segunda lei de newton para os diferentes sistemas.
Como assim sistemas?
Nós podemos analisar cada um dos três blocos separadamente (três sistemas), olhando para as forças aplicadas sobre cada um deles. Além disso, também podemos olhar para o sistema dos três blocos como um todo.
Passo 2
Vamos olhar primeiro para o sistema do bloco da frente, pois conseguimos relacionar a força com a força de tração no cabo 1 (conhecida).
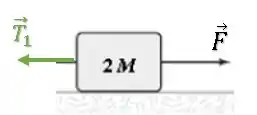
Na horizontal, temos:
Passo 3
Para encontrar outra relação, podemos olhar para o sistema como um todo.
Podemos fazer isso, porque os três blocos estão se movimentando juntos (mesma aceleração), sendo a corda 1 e 2 apenas uma ligação entre eles:
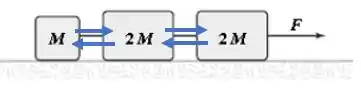
Como a força de tração é a mesma em cada corda, elas se cancelam quando olhamos para o sistema como um todo (forças internas).
Então, nós podemos pensar nos três blocos como apenas um blocão de massa igual à soma das massas sendo puxado pela força :
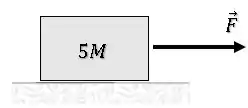
Assim, achamos uma segunda relação.
Passo 4
Ficamos com um sistema:
Podemos isolar a aceleração na segunda equação e substituí-la na primeira:
Substituindo na primeira, temos:
O enunciado diz que a força de tração no cabo 1 é de :
Ficamos com a alternativa (E).
Resposta
Letra (E)