UFABC – Sem Campus – Funções de Uma Variável – Listas – Listas FUV – GRADMAT – Lista 9 – Técnicas de Integração I – Questão 7
Ache a área da região limitada pelos gráficos de , , e .
Passo 1
Oiie, tudo bem? Vamos resolver mais uma questãozinha?
Vamos primeiro dar uma olhadinha em nossa região! Ela é a seguinte:
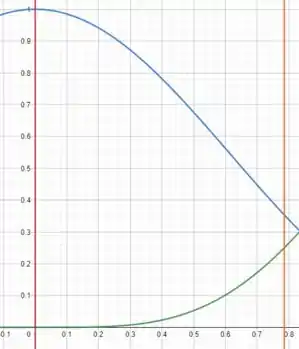
A curva azul está relacionada ao e a curva verde é o . As linhas verticais vermelha e laranja irão nos indicar os limites de integração necessários! Mas como calcularemos esta integral?
Passo 2
Temos que a integração pode ser realizada considerando a diferença:
Porque a diferença?
É que a integral de uma curva dá a área de baixo da curva. E nós queremos a área embaixo da curva azul, mas não queremos a área embaixo da curva verde (que está inclusa na área da azul). Então vamos subtrair esse pedacinho embaixo da curva verde.
Para resolver estas integrais vamos utilizar as seguintes relações:
E também que:
Vamos lá então!
Passo 3
Primeiro, vamos reescrever um tequinho nossa integral! Temos:
Se usarmos agora a equação (1) e (2), obtemos:
Ficou bem grandinho, neh? Mas agora podemos resolver algumas diretamente, e outras através de uma mudança de variáveis! Saca só!
Passo 4
Primeiro, usando a equação (2) mais uma vez, temos:
Precisamos ainda fazer uma mudança de variáveis na segunda integral em , que é a que não está em um bom formato ainda! Vamos fazer isso antes de continuar!
Passo 5
Se fizermos a mudança e , e avaliando os limites de integração, temos:
E também:
Ou seja, temos que:
Beleza! Agora podemos resolver todas elas de uma só vez!! Saca só!
Passo 6
Vamos utilizar as seguintes integrais:
Vamos com calma! Precisamos aplicar todas as quatro equações onde forem convenientes! Bora que bora!
Passo 7
Temos que:
Agora é colocar a calculadora para trabalhar! Ahahahah, mas vou ser bonzinho e te dar alguns valores importantes! Siga comigo!
Passo 8
Usando que , , , , , temos:
Poderíamos jogar isso na calculadora! Mas não tem porquê! Feshow!!! Te vejo na próxima! Tchauzinho!
