UFABC – Sem Campus – Funções de Uma Variável – Listas – Listas FUV – GRADMAT – Lista 9 – Técnicas de Integração I – Questão 5
Calcule a área da elipse .
Passo 1
Oiiie, tudo bem contigo? Bora que bora resolver mais uma?
Esse enunciado nos dá a função de uma elipse e pede pra calcularmos a área no seu interior.
A primeira coisa que seria interessante lembrar é que através de uma integração é possível calcular a área sob o gráfico de uma função! Mas neste caso, qual seria nossa função? Saca só:
Vamos usar essa função para calcular a área!
Passo 2
Para calcular a área temos que calcular a seguinte integral:
Isso nos dará um quarto da área necessária, pois estamos utilizando os limites de integração do centro da elipse até , saca só o gráfico desta função:
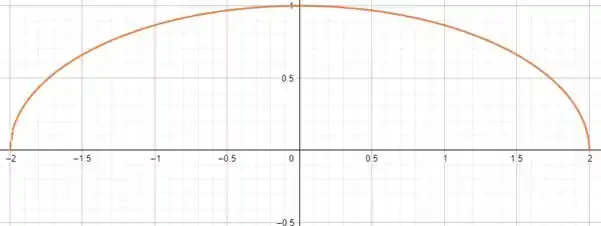
Para o gráfico, escolhi valores arbitrários de e , mas não precisamos para resolver a questão! Vamos precisar trabalhar um pouquinho a equação (1)! Vamos lá!
Passo 3
Uma maneira de fazer isso é através de uma mudança de variáveis da forma:
Para aplicar na equação (1), temos que calcular como:
Além disso, precisamos de novos limites de integração, para o limite inferior temos:
Agora, para o limite superior:
Vamos aplicar isso na equação (1)! Bora bora!
Passo 4
Nossa integral fica então como:
Beleza! Vamos tentar resolver isso agora! Bora lá!
Passo 5
Vamos começar lembrando que , ou seja, . Ou seja, a equação (2) fica como:
Podemos lembrar agora que:
E a equação (3) fica então como:
Quase lá! Agora só precisamos relembrar algumas coisinhas!
Passo 6
Lembrando as seguintes integrais:
E, também que:
Usando isso em nossa equação (4), temos que:
Mas temos que , e, portanto:
Aí está! Esta é a área de nossa elipse! A questão foi isso!
Te vejo na próxima! Tchauzinho!