UFCG, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - UAMat - Lista 3, Questão 22d
Desenhe o conjunto abaixo e calcule a área:
d) é o conjunto de todos tais que .
Passo 1
Ooi gente, tudo bom?
Precisamos desenhar e calcular a área da região que representa o conjunto . Pelo enunciado, essa região é composta por todos os pontos que obedecem a:
Quando a região vem representado por desigualdades é legal olharmos cada uma delas separadamente.
Significa que nossa região é sempre não-negativa, ou seja, está acima do eixo .
É justamente a equação de uma parábola, ou seja, nossa região é representada pelos pontos abaixo da curva da parábola e acima do eixo . Sacaram?
Então show. Vamos desenhar a região e depois usar a definição de integral pra calcular a sua área 😊
Passo 2
Bom, como vimos no passo , nossa região que representa o conjunto está abaixo da curva e acima do eixo .
A curva é uma parábola, com raízes:
Além disso, quando , temos . E, como o termo que multiplica é negativo, essa parábola está virada para baixo. Desenhando o seu esboço, temos:
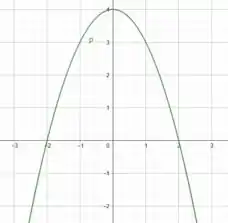
Estamos quase lá! Como nossa região está acima do eixo , podemos representá-la como:
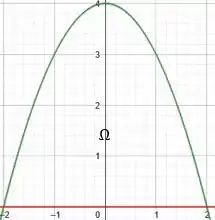
Onde a nossa região representa justamente o conjunto 😊
Passo 3
Para calcular a área dessa região, basta usarmos a definição de integral:
Nesse caso, a curva vale:
E, a região está no intervalo das raízes de , ou seja, . Logo:
Como a integral da soma é a soma das integrais:
Usando que:
Vem:
Portanto:
Prontinho! Eaí, curtiram a solução? Responde Aí 😊