Desenhe o conjunto abaixo e calcule a área:
h) é o conjunto do plano limitado pelas retas , e pelo gráfico de .
Passo 1
Faaala pessoal!
Nessa questão temos uma região que é limitada pelas curvas:
Sobre essa região precisamos desenhá-la e calcular a sua área.
Para desenhá-la precisaremos analisar como essas curvas estão definindo a região. Já pra calcular a sua área precisamos lembrar do que significa uma integral. Vocês lembram?

Ela é justamente a área entre a curva e o eixo .
Show! Então vamos lá 😊
Passo 2
As equações e representam duas retas verticais, que passam respectivamente por e .
A reta , como já comentamos, é o próprio eixo .
Por fim,
é a equação de uma parábola. Para esboçá-la junto com as outras curvas, vamos antes calcular suas raízes:
Por bháskara, para um polinômio do tipo:
Temos:
Usando essa expressão na nossa equação do grau:
Cujas raízes são complexas, indicando que a parábola está toda acima do eixo .
Logo, esboçando a nossa região, temos:
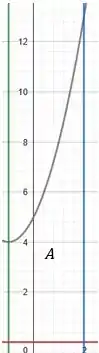
Prontinho!
Passo 3
Agora, vamos calcular a área através da integral.
Como comentamos anteriormente, a área entre uma curva e o eixo é dada por:
Como na nossa região , no intervalo de a curva está toda acima do eixo , ou seja, , teremos:
Usando que a integral da soma é a soma das integrais e também que:
Chegamos a:
Portanto:
Conseguimossss!! Até a próxima gente 😊