UFCG, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - UAMat - Lista 3, Questão 22c
Desenhe o conjunto abaixo e calcule a área:
c) é o conjunto de todos tais que .
Passo 1
Oláaaa, todo mundo animadoo? Vamo lá!!!
Temos um conjunto , que basicamente é uma região no plano , dos pontos que obedecem a equação:
Essa equação lembra vocês de alguma curva conhecida?
Se analisarmos essas desigualdades separadamente, fica mais fácil de enxergar:
é a equação de uma parábola. Queremos os pontos acima (ou em cima) da parábola, mas que ainda obedeçam a .
Massa! Esse é o nosso conjunto . O enunciado nos pede para desenhar a região desses pontos e calcular a sua área. Então vamo lá?!
Passo 2
Pra desenhar essa região que representa o conjunto , vamos começar esboçando a parábola.
Primeiro vamos calcular as suas raízes para aí sim esboçá-la:
Além disso, quando , . Assim:
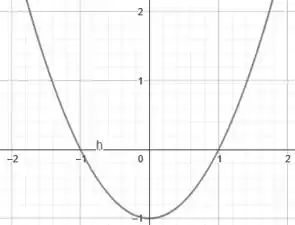
Como comentamos no passo anterior, pela desigualdade do enunciado, temos também:
Assim, os pontos que estão acima dessa parábola, mas ainda são não-positivos, formam a região:
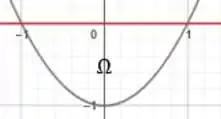
Perfeito! Conseguimos desenhar a nossa região 😊
Passo 3
Agora vamos calcular a área de . Para fazer isso, devemos lembrar que a área entre uma curva e o eixo é dada por:
Se for menor do que no intervalo , então teremos:
Como nesse caso a curva é justamente a parábola , e que pela outra desigualdade que lhe descreve:
é não-positiva na região , vamos utilizar justamente a expressão com o sinal negativo. Além disso, essa região está no intervalo entre as raízes da parábola, ou seja:
Assim, escrevendo a integral:
Como a integral da soma é a soma das integrais:
Usando que:
Temos:
Portanto:
Uhuuul! Matamos mais uma questão!
Espero que vocês tenham entendido beeem direitinho, até a próxima pessoal 😊