UFABC – Sem Campus – Funções de Uma Variável – Listas – Listas FUV – GRADMAT – Lista 9 – Técnicas de Integração I – Questão 8
A região sob o gráfico de no intervalo é girado em torno do eixo . Encontre o volume do sólido gerado.
Passo 1
Eaew, tudo certinho com você hoje?
E agora, meu senhor? Como que faço uma rotação de um gráfico de em torno do eixo ?? Não se desespere jovem padawan! Temos que fazer o seguinte:
Conhecido como método das cascas cilíndricas! A região que iremos rotacionar é a seguinte:
Após rotacionar obtemos algo como isso:
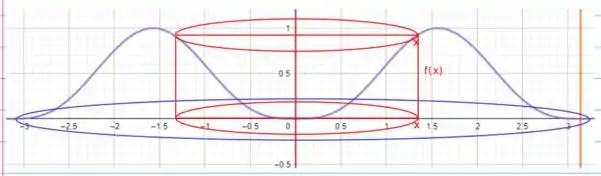
Agora só precisamos utilizar o esquema acima para calcular o nosso volume! Beleza?
Passo 2
Primeiro, podemos identificar que o raio é sempre o valor escolhido em e também que a altura do cilindro escolhido é a própria função. Desse jeitinho aqui:
Agora o problema se torna calcular essa integral (Admita que melhorou um pouquinho!!! Ahahahah) E nós vamos resolver ela por partes!! Bora lá!
Passo 3
Vamos escolher como nosso e o nosso , de forma que temos:
E também:
Aiai... mas e agora? Para obter este precisamos utilizar algumas relações trigonométricas! Vem comigo!
Passo 4
Vamos utilizar:
Obtendo:
Quase lá agora! A primeira integral em cima é só olhar em seu formulário e lembrar que:
Lembre que a constante de integração pode ser ignorada por enquanto já que vamos aplicar os limites de integração ao finalizar a integração por partes! Belezinha?
Passo 5
Agora vamos para a segunda integral em (1), vamos utilizar a substituição e , ou seja, temos:
Lembrando que:
Temos:
Vamos substituir isso na nossa integral! Hehehehe
Passo 6
Colocando (2) e (3) em (1), temos:
Se lembrarmos que a integração por partes é dada da seguinte forma:
Temos:
Vamos continuar trabalhando ela um pouquinho! Respira e bora lá!
Passo 7
A segunda integral pode ser obtida utilizando:
Mas, a última integral que sobrou em (5) requer que utilizemos que e uma mudança de variáveis! Devagarzinho saí! Vamos que vamos!
Passo 8
Temos então:
Acabamos de ver que a primeira integral dá zero! Ótimo!!! Para a segunda podemos fazer a substituição e , de forma que temos:
Como fizemos anteriormente, temos que:
Como a maioria das coisas zeraram! Sobra só um restinho para se calcular no nosso volume! Vem comigo!
Passo 9
Temos então que:
Como temos que e , temos:
Acabou... meu deus senhor! Aleluia!! Te vejo na próxima!
