Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área de Superfícies de Revolução

Ver Teoria
Exercício 31245678910111213141516171819202122232425262728293031323334353637383940414243444546

Enunciado

Determine as áreas das superfícies geradas pela rotação da curvas em torno dos eixos indicados.

x = 2 y - 1 ,     5 8 ≤ y ≤ 1 ,     e i x o   y

Passo 1

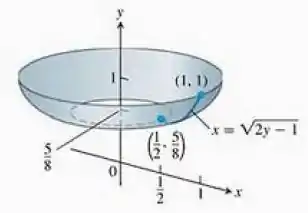
Queremos a área da superfície de revolução gerada pela rotação da curva x = 2 y - 1 em torno do eixo y no intervalo 5 8 ≤ y ≤ 1 . A função é derivável em todo o intervalo.

Portanto, tudo o que temos que fazer é utilizar aquela fórmula esperta de área usada para quando queremos a área da superfície lateral quando temos uma rotação em torno do eixo y :

S =   ∫ c d 2 π x   1 + g ´ y 2 d y = ∫ c d 2 π g ( y )   1 + g ´ y 2   d y

Passo 2

Vamos achar os elementos da integral.

Temos

g y =   2 y - 1 → g ´ y = 2   . 1 2 2 y - 1 - 1 2 = 2 y - 1 - 1 2

g ´ y 2 = 2 y - 1 - 1 = 1 2 y - 1

S = ∫ 5 8 1 2 π x   1 + 1 2 y - 1   d y

S = ∫ 5 8 1 2 π 2 y - 1   1 + 1 2 y - 1   d y

Passo 3

Agora temos que resolver essa integral aí.

Olha só o que eu vou fazer. Vou juntar os dois termos que estão dentro da raiz:

S = ∫ 5 8 1 2 π 2 y - 1 1 + 1 2 y - 1   d y

S = ∫ 5 8 1 2 π 2 y - 1 + 1   d y

S = ∫ 5 8 1 2 π 2 y   d y

S = 2 π 2 ∫ 5 8 1 y 1 2   d y

S = 2 π 2 . 2 3 y 3 2 5 / 8 1

S = 4 π 2 3   1 3 2 - 5 8 3 2 = 4 π 2 3 1 - 5 3 2 8 3   2  

Vamos dar uma arrumada nesse valor

S = 4 π 2 3 1 - 5 2 . 5   2 2 3 3 2 = 4 π 2 3 1 - 5   5 2 9 2 =     4 π 2 3 1 - 5   5 2 8 . 2 2    

S = 4 π 2 3 1 - 5   5 2 4 . 2 =     4 π 2 3 1 - 5   5 16 2

S = 4 π 2 3 16 2 - 5 5 16 2

S = π 12 16 2 -   5 5

Resposta

S = π 12 16 2 -   5 5 u . a .

Exercícios de Livros Relacionados

Encontre a área da superfície gerada quando a curva dada gira em torno do eixo x . x =y 3 , 1 ≤ y ≤ 8
Mostre que a área das superfícies de uma zona de uma esfera que está entre dois planos paralelos é S = 2 π R h , onde R é o raio da esfera e h , a distância entre os planos. (Observe que S depende ape
Calcule a área da superfície obtida pela rotação da curva em torno do eixo x x = 1 + 2 y 2 , 1 ≤ y ≤ 2
Use a regra de Simpson com n = 10 para aproximar a área da superfície obtida pela rotação da curva em torno do eixo x . Compare o seu resultado com o valor da integral obtido em sua calculadora y = se
Use o resultado do exercício 31 para escrever uma integral para encontrar a área da superfície gerada pela rotação da curva y = x ,0 ≤ x ≤ 4 , em torno da reta y = 4 . Então, use um SCA para calcular