UFCG, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - UAMat - Lista 3, Questão 22l
Desenhe o conjunto abaixo e calcule a área:
l) e
Passo 1
Faaaaala galera, quem tá animado pra resolver essa questãooo?
Hahaha! Vem comigo que vai dar certo 😊
Aqui temos um conjunto que é dado no enunciado em uma linguagem bem matemática:
e
Entendi nada, quem que é mesmo? hahaha
Calma lá! Basicamente, ela é o conjunto de todos os pontos que estão no intervalo em de a , e em são limitados pelas curvas:
Sacaram? Fica tranquilo, uma das coisas que precisamos fazer é desenhar a região . Aí vai ficar mais claro isso que estamos comentando.
Além disso, também precisamos calcular a sua área. Como se trata de uma região limitada por duas curvas, a ideia é usar uma operação entre áreas, fazendo:
onde e são áreas escolhidas convenientemente entre uma curva e o eixo . Ou seja:
Sacaram?
Então bora lá!
Passo 2
Vamos começar desenhando a nossa região . Ela é limitada pelas curvas:
é uma reta horizontal que passa por .
é uma curva com a seguinte cara:
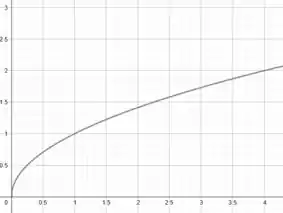
Assim, como a nossa região está limitada em no intervalo , plotando tudo no mesmo gráfico, temos:
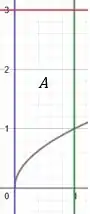
Show! Conseguiram entender quem é a região ?
Passo 3
Bom, continuando, vamos agora calcular a sua área.
Basicamente, precisamos fazer uma subtração entre a área abaixo da reta e da curva .
Como comentamos no passo , a área abaixo dessas curvas e acima do eixo , vale:
onde é a área abaixo de e é a área abaixo de .
Assim, podemos dizer que:
Vamos então calculá-las!
Usando que:
Vem:
Já para , temos:
Usando novamente a regra de integração monomial:
Juntando as duas áreas, temos:
Ou seja:
E é isso gente, terminamos!! Muito obrigado pela atenção, tmj! 😊