UFCG, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - UAMat - Lista 3, Questão 22p
Desenhe o conjunto abaixo e calcule a área:
p) é o conjunto de todos os pontos tais que e .
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu um conjunto de pontos que estão entre a reta e a parábola , e pediu pra gente desenhar esse conjunto e calcular a área dele. Por onde a gente começa?
Vamos começar desenhando a parábola , acrescentar a reta , encontrar os pontos de intersecção das duas curvas e calcular a área requerida usando uma integral definida.
Então, vamos lá!
Passo 2
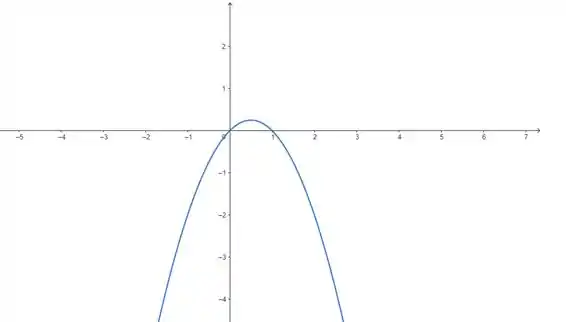
Galera, repara que na nossa parábola , quando , também é igual a . Isso significa que ela passa pela origem. Agora, quando , nós temos:
Então, além do ponto , curva também passa pelo ponto . Ela tem concavidade virada pra baixo, porque o coeficiente do é negativo.
Com essas informações, a gente consegue plotar a curva:
Beleza, agora vamos plotar a reta , que tem uma inclinação negativa, então ela vai ser assim: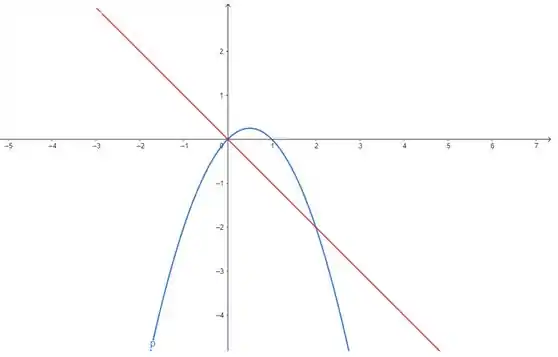
Repara que as nossas curvas se encontram em e em algum outro ponto ali embaixo no gráfico. Mas a gente pode verificar isso fazendo:
Vamos calcular as raízes dessa equação pra encontrar os pontos de interseção.
Colocando em evidência, temos:
Logo,
Então, tudo certo, esses são nossos pontos de interseção e é nesse intervalo que nós vamos integrar para encontrar a área .
Passo 3
Vamos montar nossa integral (sempre fazendo a curva que tá por cima menos a curva que tá por baixo no intervalo):
Integrando, temos:
Substituindo os intervalos de integração:
E encontramos nossa área!
Até a próxima, galera! 😉