UFCG, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - UAMat - Lista 3, Questão 22g
Desenhe o conjunto abaixo e calcule a área:
g) é o conjunto do plano limitado pela reta e pelo gráfico de , com .
Passo 1
Faaaala pessoal, tudo beleza?
Precisamos desenhar e calcular a área da região que representa o conjunto . Esse conjunto contém todos os pontos entre a parábola:
e o eixo , no intervalo .
Alguma ideia pra calcular essa área ?
Para fazer isso, devemos lembrar que a área entre uma curva e o eixo é dada por:
Se for menor do que no intervalo , então teremos:
Show! Vamos começar desenhando a parábola e depois usamos a integral para calcular sua área.
Passo 2
Como comentamos no passo anterior, a região do conjunto está entre uma parábola e o eixo . Essa parábola tem equação:
Já que o termo que multiplica é negativo, a parábola está virada para baixo. Para desenhá-la, vamos antes buscar encontrar as raízes:
Por bháskara, para um polinômio do tipo:
Temos:
Usando essa expressão na nossa equação do grau:
Logo, esboçando a nossa parábola:
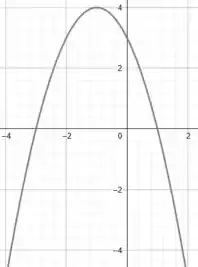
Massa! Como a nossa região de interesse está no intervalo , temos:
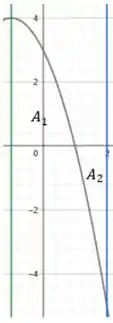
Passo 3
Para calcular a sua área, como no intervalo a curva assume valores positivos em e negativos em , devemos usar que:
Lembrando do que comentamos no passo :
Vamos ter:
E:
Logo:
Como a integral da soma é a soma das integrais, e usando que:
Vem:
Substituindo os limites de integração:
Portanto:
Uhuuul! Terminamos. Vocês curtiram? Responde Aí!