UFCG, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - UAMat - Lista 3, Questão 22e
Desenhe o conjunto abaixo e calcule a área:
e) é o conjunto de todos tais que , com .
Passo 1
Oooi pessoal, tudo certinho?
Aqui temos um conjunto , que basicamente é uma região no plano , que satisfaz a seguinte inequação:
no intervalo .
Precisamos desenhar essa região e calcular a sua área.
Vocês estão lembrados do significado da integral abaixo?
Ela é justamente a área entre a curva e o eixo . É isso que vamos usar pra calcular a área da nossa região. Então, vamos lá!
Passo 2
Bom, como vimos no passo , a nossa região é determinada pelas desigualdades:
no intervalo de a .
Então, bora esboçar o gráfico do nesse intervalo e ver quais partes se enquadram na desigualdade.
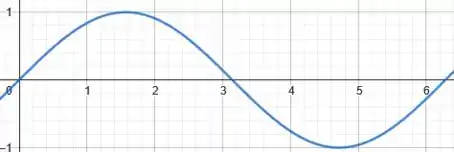
Como na desigualdade:
temos o módulo no , toda região no intervalo de a obedece a:
Portanto, a região que representa a área é composta pela união de e :
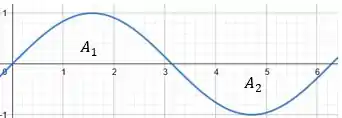
Prontinho, perfeito!
Passo 3
Agora precisamos calcular a área total dessa região.
Como vimos no passo , a área entre uma curva e o eixo é dada por:
Na região , temos , logo:
Já na região , temos , logo:
Logo, a área total de , vale:
Lembrando que a primitiva do é , temos:
Portanto:
Boaaaaa! Terminamos gente, vocês entenderam tudinho?É isso então, até a próxima 😊