UFCG, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - UAMat - Lista 3, Questão 22b
Desenhe o conjunto abaixo e calcule a área:
b) é o conjunto do plano limitado pelas retas , , e pelo gráfico .
Passo 1
Ooii galerinha do bem, tudo tranquilo com vocês?
O enunciado nos dá um conjunto no plano (que nada mais é do que uma região), limitado pelas curvas:
Precisamos desenhar essa região e calcular a sua área.
Vocês lembram como podemos calcular essa área?
Basta usarmos a própria definição da integral, que representa a área abaixo de uma curva em um intervalo de :
Prontinho, agora que já revisamos, vamos colocar a mão na massa! Primeiro desenhamos a região e depois calculamos a sua área através da integral.
Passo 2
Como vimos no passo anterior, o conjunto é uma região no plano limitado por:
e são duas retas verticais passando por e respectivamente.
é o próprio eixo .
Já a curva tem um formato do tipo:
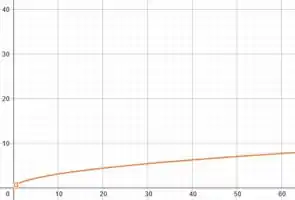
Juntando todas essas curvas em um mesmo gráfico, podemos identificar a região que representa a o conjunto , como:
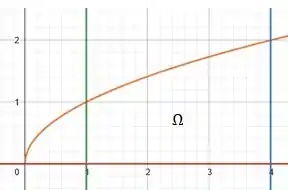
Perfeito 😊
Passo 3
Agora precisamos apenas calcular a área que representa essa região. Lembrando que:
E aqui temos no intervalo , e que a região é a curva abaixo de , temos . Portanto:
Usando que:
Temos:
Por fim:
Aeee, conseguimos!! Boa pessoal 😊