Desenhe o conjunto abaixo e calcule a área:
m) é o conjunto do plano limitado pelas retas , e pelos gráficos de e .
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu um plano limitado pelas retas , e pelas curvas de e . Nós precisamos plotar essas curvas e calcular a área limitada por elas.
Mas por onde começar? Vamos começar desenhando as curvas de e , acrescentar as retas e , encontrar os pontos de intersecção das curvas e calcular a área requerida usando uma integral definida.
Então, vamos lá!
Passo 2
Vamos plotar as curvas seno e cosseno:
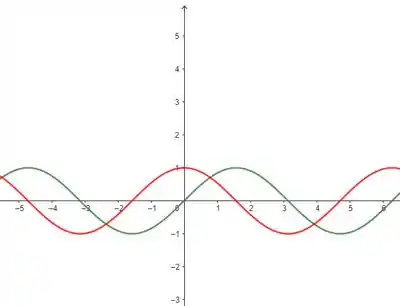
A curva em vermelho é e, em verde, temos . Agora vamos acrescentar as retas e limitar nossa área horizontalmente:
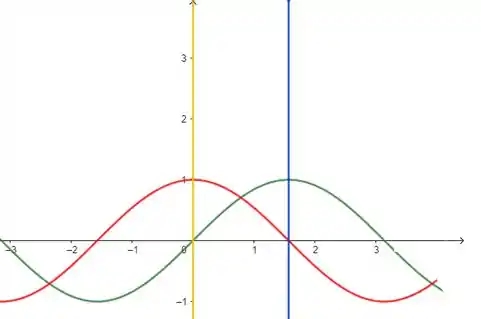
Em amarelo nós temos a reta e em azul a reta . Beleza, então nossa área pode ser dividida em duas, de até a interseção das curvas e da interseção até . Só falta a gente descobrir onde essas curvas se cruzam.
Passo 3
Os pontos de interseção ocorrem quando , isso acontece quando (considerando o intervalo ). Então nossa região fica assim:
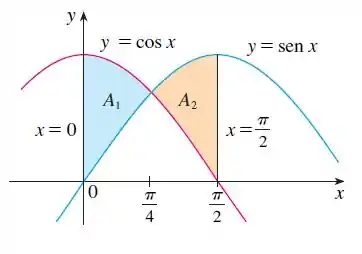
Repara que a curva do cosseno tá por cima, quando , mas a curva do seno fica acima quando . Então a nossa área vai ser dada por duas integrais, considerando esses dois intervalos. Assim:
Calculando as integrais, temos:
Aplicando os intervalos de integração:
Calculando, temos:
Ou
E encerramos o exercício! Até a próxima, galera! 😉