UFCG, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - UAMat - Lista 3, Questão 22k
Desenhe o conjunto abaixo e calcule a área:
k) é o conjunto do plano limitado pela reta , pelo gráfico , com .
Passo 1
Oi gente, tudo bem?
Nesse item temos uma região que é limitada por duas curvas:
Precisamos desenhar o seu esboço e também calcular a sua área.
Um ponto de dificuldade nesse exercício é que, quando usamos a integral para calcular área, estamos calculando a área entre uma curva e o eixo . Mas, aqui precisamos calcular uma área entre duas curvas. O que podemos fazer?
Em geral, nesse tipo de problema a ideia é usar uma operação entre áreas, fazendo:
onde e são áreas escolhidas convenientemente entre uma curva e o eixo . Ou seja:
Sacaram?
Bom, essa vai ser a ideia principal. Então, vamos lá 😊
Passo 2
Começando pelo desenho da nossa região, temos que ela é limitada por:
É importante calcularmos os pontos de intersecção entre essas duas curvas:
Logo:
Assim, entre e , temos que é maior do que . Para ver isso, podemos fazer um teste:
Já entre e a relação se inverte, e (uma reta) é maior do que (curva do monômio cúbico). Novamente:
Assim, esboçando a região temos:
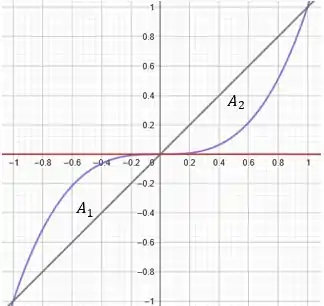
onde a nossa região é composta pela união de e de .
Passo 3
Beleza. Já pra calcular a área total vamos usar a ideia que comentamos no passo . Primeiro, como é composta pela união de e de :
Já é calculada pela subtração das áreas entre a reta (em módulo ) e . Assim:
Usando que:
Vem:
Logo:
Novamente, para calculamos pela subtração entre a área abaixo da reta e a área abaixo da reta . Assim:
Logo:
Por fim, juntando tudo, temos:
Prontinhoo! Matamos mais uma 😊
Vamo simboraaa!!