Dadas as superfícies e de equações e , respectivamente, obtenha uma parametrização da curva formada pela interseção de com e que está localizada acima do plano .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

Foram dadas duas superfícies descritas como e .
Com essas duas superfícies, temos que obter uma curva gerada pela intersecção entre e que esteja acima do plano .
Tem ideia de como fazemos isso? 🤔🤔
Temos que encontrar uma forma de igualar e . Se isolarmos em um lado das duas equações, temos um bom início, não acha?
Depois que encontrar essa equação, vamos tentar parametriza-la reescrevendo suas variáveis em um número menor de variáveis
Bora começar! 😎
Passo 2
Primeiro vamos isolar da superfície
Isolando da superfície
Igualando as duas equações, temos
Com isso, encontramos
A intersecção das duas superfícies gera uma elipse com o centro em , e
Interessante, não é? 😁
Passo 3
Agora, por fim, vamos parametrizar essa equação.
A parametrização de uma curva funciona como um ocultador de variáveis. No caso, temos duas variáveis na equação ( e ) então vamos reescreve-la como uma única variável só.
Se considerarmos , temos
Vamos isolar em um lado da igualdade
Tirando a raiz dos dois lados dado que , vamos obter
pode ser negativo ou positivo, então temos que considerar como sendo positivo ou negativo fazendo
Com isso, podemos obter uma parametrização da elipse que encontramos dado que e .
Essa equação é a projeção da intersecção das superfícies no plano . Se plotarmos essa equação, temos
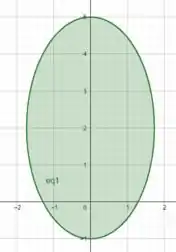
Com isso, obtemos também o gráfico da intersecção de com !
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
