UFCG, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - UAMat - Lista 3, Questão 22i
Desenhe o conjunto abaixo e calcule a área:
i) é o conjunto do plano limitado pelas retas e pelo gráfico de
Passo 1
Eaí galera, tudo tranquilo?
Nessa questão temos uma região que é limitada pelas curvas:
Sobre essa região precisamos desenhá-la e calcular a sua área.
Para calcular a área de uma região podemos usar o recurso da integral. Pois, a área entre uma curva e o eixo é dada por:
Então, vamos começar esboçando a área dessa região e depois calculamos a sua área através da integral.
Passo 2
Temos que a nossa região é limitada por:
As retas e representam os eixos e , respectivamente,
é uma reta vertical que passa por .
E, é nossa famosa função trigonométrica.
Esboçando todas elas em um mesmo gráfico, temos:
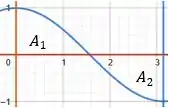
Prontinho, a nossa região é a união de e .
Passo 3
Para calcular a sua área basta usarmos o recurso da integral:
Como a nossa região , ora possui positiva, ora negativa, no intervalo , vamos dividir o seu cálculo. Fazendo:
Na região , que vai de a , temos . Assim:
Já na região , que vai de a , temos . Logo:
Juntando:
Logo:
E é isso gente! Agora vamo dar aquela pausa pra beber uma água, tomar um café, e já volta com tudo no próximo item 😊