UFCG, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - UAMat - Lista 3, Questão 22j
Desenhe o conjunto abaixo e calcule a área:
j) é o conjunto de todos tais que e .
Passo 1
Eaí povo, tudo na paz?
Temos aqui um conjunto , que é uma região que possui todos os pontos que obedecem às seguintes desigualdades:
Precisamos desenhar e calcular a sua área.
Alguma ideia de como fazer isso?
Pra desenhar a região, quando ela é definida por várias desigualdades, a ideia é analisar cada uma delas vendo suas implicações na limitação geométrica da região.
Já para o cálculo da área, devemos usar que a área entre uma curva determinada por e o eixo é dada por:
Massa! Então vamos lá, mãos à obra 😊
Passo 2
Começando pelo desenho da área , vemos que a região é determinada por:
A primeira desigualdade significa que nossa região está à direita do eixo .
Temos também que:
Ou seja, os pontos que nos interessam são aqueles que estão limitados pelas curvas:
Suas intersecções ocorrem em:
Logo:
Como temos , apenas as duas últimas intersecções nos interessam.
é uma reta que passa pela origem.
é a curva do polinômio cúbico.
Plotando tudo isso no mesmo gráfico, temos:
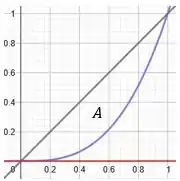
Excelente!
Passo 3
Agora vamos calcular a sua área!
Puts, a fórmula que a gente viu relaciona a área entre uma curva e o eixo , mas aqui temos que calcular a área entre duas curvas. O que fazemos?
Calma aí galera! Podemos usar uma ideia de superposição, ou de subtração entre áreas.
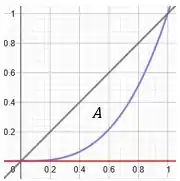
Se analisarmos bem, a nossa área é a subtração da área abaixo da reta e acima do eixo , pela área abaixo da curva e acima do eixo . Essas duas áreas sabemos como calcular!
Portanto:
Usando que:
Vem:
Portanto:
Ufaaaa! Terminamos. Vamo pra próxima 😊