UFCG, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - UAMat - Lista 3, Questão 22f
Desenhe o conjunto abaixo e calcule a área:
f) é a região do plano compreendida entre o eixo e o gráfico de , com .
Passo 1
Oi oi oi galera, quem aí tá preparado pra matar mais uma questãozita?
Aqui temos uma região , que está abaixo da curva:
no intervalo .
Precisamos desenhar a região , bem como calcular a sua área.
Vocês lembram como podemos calcular essa área?
Basta usarmos a própria definição da integral, que representa a área entre uma curva e o eixo , no intervalo de :
Prontinho! Mãos à obra!!
Passo 2
Bom, essa nossa curva:
É a equação de uma parábola. Sempre que precisamos desenhar esse tipo de curva, é legal conhecermos onde estão as suas raízes. Assim:
Logo, temos duas raízes:
A nossa região está justamente entre a parábola e o eixo no intervalo . Assim, podemos desenhá-la:
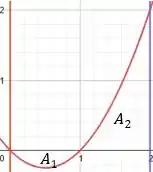
Prontinho, a nossa região é a união de e de
Passo 3
Agora, vamos calcular a área da região .
Como vimos no passo , a área entre uma curva e o eixo é dada por:
Na região , temos , logo:
Já na região , temos , logo:
Assim, a área total , vale:
Usando que:
Temos:
Portanto:
E, é isso gente! Obrigado pela atenção 😊