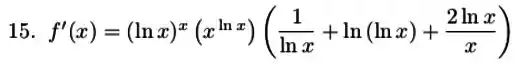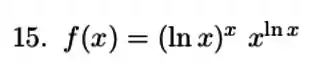
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Derivação Logarítmica

Ver Teoria
Exercício 22123456789101112131415161718192021232425262728293031323334353637383940414243444546474849505152

Enunciado

Passo 1

Começamos usando a Regra do Produto nesse termo aí:

f x = ln ⁡ x x x ln ⁡ x

= ln ⁡ x x ' x ln ⁡ x + ln ⁡ x x x ln ⁡ x '

Vamos usar a derivação logarítmica pra cada um dos termos!

Passo 2

Na primeira das derivadas, teremos:

y = ln ⁡ x x → ln ⁡ y = ln ⁡ ln ⁡ x x

Podemos botar o expoente para frente

ln ⁡ y = x ln ⁡ ln ⁡ x

Agora é só fazer a derivação implícita:

y ' y = x ' ln ⁡ ln ⁡ x + x ln ⁡ ln ⁡ x '

y ' y = 1 ln ⁡ ln ⁡ x + x ln ⁡ x ' ln ⁡ x

y ' y = ln ⁡ ln ⁡ x + x 1 x ln ⁡ x

y ' = y ln ⁡ ln ⁡ x + 1 ln ⁡ x

Porém, y = ln ⁡ x x . Então,

y ' = ln ⁡ x x 2 x ln ⁡ x + x

Passo 3

Na primeira das derivadas, teremos:

y = x ln ⁡ x → ln ⁡ y = ln ⁡ x ln ⁡ x

Podemos botar o expoente para frente

ln ⁡ y = ln ⁡ x ln ⁡ x = ln ⁡ x 2

Agora é só fazer a derivação implícita:

y ' y = ln ⁡ x 2 ' = 2 ln ⁡ x ln ⁡ x '

y ' = y 2 ln ⁡ x 1 x

Porém, y = x ln ⁡ x . Então,

y ' = x ln ⁡ x 2 ln ⁡ x x

Passo 4

Assim, ficamos com:

f ' x = ln ⁡ x x ' x ln ⁡ x + ln ⁡ x x x ln ⁡ x '

= ln ⁡ x x 2 x ln ⁡ x + x x ln ⁡ x + ln ⁡ x x x ln ⁡ x 2 ln ⁡ x x

= ln ⁡ x x x ln ⁡ x 2 x ln ⁡ x + x + 2 ln ⁡ x x

Resposta

Exercícios de Livros Relacionados

Mostre que underset(n - oo)(lim) (1 + (x)/(n))^n = e^x , para qualquer xo
Nos exercícios 55-62, determine a derivada de y com relação a x , t ou θ , conforme o caso y = ln ⁡ ( 3 θ e - θ )
Nos exercícios 55-62, determine a derivada de y com relação a x , t ou θ , conforme o caso y = ln ⁡ ( 2 e - t sen ⁡ t )
Nos exercícios 41-54, utilize a derivação logarítmica para determinar a derivada de y em relação à variável independente dada. y = x 2 + 1 x - 1 2
Nos exercícios 41-54, utilize a derivação logarítmica para determinar a derivada de y em relação à variável independente dada. y = t ( t + 1 ) ( t + 2 )