Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Derivação Logarítmica

Ver Teoria
Exercício 71234568910111213141516171819202122232425262728293031323334353637383940414243444546474849505152

Enunciado

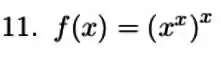
Passo 1

Vamos usar a derivação logarítmica, mas antes usamos uma propriedade de exponenciais para escrever em só uma potência o termo:

y = x x x = x x . x = x x 2

Então, derivamos por logaritmo:

y = x x 2 → ln ⁡ y = ln ⁡ x x 2

Podemos botar o expoente para frente

ln ⁡ y = x 2 ln ⁡ x

Agora é só fazer a derivação implícita:

y ' y = x 2 ' ln ⁡ x + x 2 ln ⁡ x '

y ' y = 2 x ln ⁡ x + x 2 1 x

y ' y = 2 x ln ⁡ x + x

y ' = y 2 x ln ⁡ x + x

Porém, y = x x x . Então,

y ' = x x x 2 x ln ⁡ x + x

Resposta

Exercícios de Livros Relacionados

Mostre que underset(n - oo)(lim) (1 + (x)/(n))^n = e^x , para qualquer xo
Nos exercícios 55-62, determine a derivada de y com relação a x , t ou θ , conforme o caso y = ln ⁡ ( 3 θ e - θ )
Nos exercícios 55-62, determine a derivada de y com relação a x , t ou θ , conforme o caso y = ln ⁡ ( 2 e - t sen ⁡ t )
Nos exercícios 41-54, utilize a derivação logarítmica para determinar a derivada de y em relação à variável independente dada. y = x 2 + 1 x - 1 2
Nos exercícios 41-54, utilize a derivação logarítmica para determinar a derivada de y em relação à variável independente dada. y = t ( t + 1 ) ( t + 2 )