Listas de Eletromagnetismo - UFMG de Fundamentos de Eletromagnetismo da UFMG - Lista de Fundamentos de Eletromagnetismo
Fundamentos de Eletromagnetismo - UFMG
Considere quatro cargas pontuais colocadas nos vértices de um quadrado de lado como mostrado na figura abaixo.
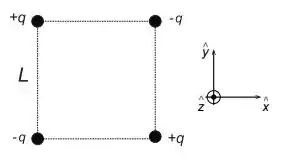
Calcule:
A energia potencial do sistema.
Ver solução completaConsidere quatro cargas pontuais colocadas nos vértices de um quadrado de lado como mostrado na figura abaixo.
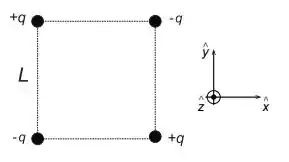
Calcule:
A força sobre a carga situada no vértice superior direito.
Ver solução completaConsidere quatro cargas pontuais colocadas nos vértices de um quadrado de lado como mostrado na figura abaixo.
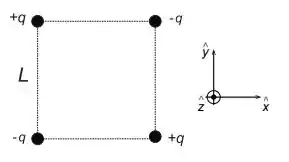
Calcule:
A força sobre a carga situada no vértice superior direito.
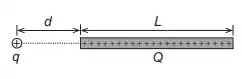
Ver solução completaUm fio infinito com densidade linear de carga positiva está posicionado a uma distância da ponta de um bastão de comprimento com carga positiva uniformemente distribuída ao longo de toda sua extensão, conforme mostrado na figura abaixo. Calcule o módulo da força de repulsão exercida sobre o bastão.
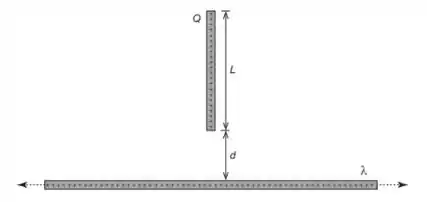
Uma carga pontual positiva está posicionada a uma distância da ponta de um bastão de comprimento com carga positiva uniformemente distribuída ao longo de toda sua extensão, conforme mostrado na figura abaixo. Calcule o módulo da força de repulsão exercida sobre a carga .
Um cilindro infinitamente longo e de raio está carregado uniformemente em toda a sua extensão, sendo a densidade volumétrica de carga. Calcule:
O módulo do campo elétrico a uma distância do eixo do cilindro.
Ver solução completaUm cilindro infinitamente longo e de raio está carregado uniformemente em toda a sua extensão, sendo a densidade volumétrica de carga. Calcule:
O módulo do campo elétrico a uma distância do eixo do cilindro.
Ver solução completaConsidere uma casca esférica com raio interno e raio externo , carregada uniformemente com densidade de carga , onde é uma constante e é a distância ao centro.
Calcule o módulo do campo elétrico para:
Ver solução completa
Considere uma casca esférica com raio interno e raio externo , carregada uniformemente com densidade de carga , onde é uma constante e é a distância ao centro.
Calcule o módulo do campo elétrico para:
Ver solução completa
Considere um capacitor formado por duas placas paralelas quadradas de lado , colocadas a uma distância uma da outra, sendo . Calcule:
O módulo do campo elétrico entre as placas, em regiões distantes das bordas.
Ver solução completaConsidere um capacitor formado por duas placas paralelas quadradas de lado , colocadas a uma distância uma da outra, sendo . Calcule:
A diferença de potencial entre as placas.
Ver solução completaConsidere um capacitor formado por duas placas paralelas quadradas de lado , colocadas a uma distância uma da outra, sendo . Calcule:
A capacitância do capacitor.
Ver solução completaAs duas placas de um capacitor esférico possuem raios e , com . Considerando que há vácuo entre as placas, e que as placas interna e externa possuem cargas e , respectivamente, calcule:
O módulo do campo elétrico a uma distância do centro, para e .
Ver solução completaAs duas placas de um capacitor esférico possuem raios e , com . Considerando que há vácuo entre as placas, e que as placas interna e externa possuem cargas e , respectivamente, calcule:
A diferença de potencial entre as placas
Ver solução completaAs duas placas de um capacitor esférico possuem raios e , com . Considerando que há vácuo entre as placas, e que as placas interna e externa possuem cargas e , respectivamente, calcule:
A capacitância do capacitor.
Ver solução completaAs duas placas de um capacitor esférico possuem raios e , com . Considerando que há vácuo entre as placas, e que as placas interna e externa possuem cargas e , respectivamente, calcule:
A energia armazenada no capacitor.
Ver solução completaRefaça todos os itens do problema anterior, considerando agora que a região entre as esferas é preenchida com um material dielétrico de constante dielétrica .
Ver solução completaDois cilindros metálicos, concêntricos, infinitamente longos e de raios e atuam como placas de um capacitor cilíndrico. Considerando que há vácuo entre as placas, e que as placas interna e externa possuem densidade linear de carga e , respectivamente, calcule:
O módulo do campo elétrico a uma distância do centro, para e .
Ver solução completaDois cilindros metálicos, concêntricos, infinitamente longos e de raios e atuam como placas de um capacitor cilíndrico. Considerando que há vácuo entre as placas, e que as placas interna e externa possuem densidade linear de carga e , respectivamente, calcule:
A diferença de potencial entre as placas.
Ver solução completaDois cilindros metálicos, concêntricos, infinitamente longos e de raios e atuam como placas de um capacitor cilíndrico. Considerando que há vácuo entre as placas, e que as placas interna e externa possuem densidade linear de carga e , respectivamente, calcule:
A capacitância de um comprimento de segmento do capacitor.
Ver solução completaDois cilindros metálicos, concêntricos, infinitamente longos e de raios e atuam como placas de um capacitor cilíndrico. Considerando que há vácuo entre as placas, e que as placas interna e externa possuem densidade linear de carga e , respectivamente, calcule:
A energia armazenada em um segmento de comprimento do capacitor.
Ver solução completaRefaça todos os itens do problema anterior, considerando agora que a região entre cilindros é preenchida com um material dielétrico de constante dielétrica .
Ver solução completaUma esfera oca de raio interno e raio externo é feita de um material de resistividade . As paredes internas e externa dessa esfera são metalizadas. Supondo que seja muito maior que a resistividade do metal depositado, calcule a resistência elétrica entre as paredes interna e externa.
Ver solução completaUm cilindro oco de comprimento raio interno e raio externo é feito de um material de resistividade . As paredes internas e externa desse cilindro são metalizadas. Supondo que seja muito maior que a resistividade do metal depositado, calcule a resistência elétrica entre as paredes interna e externa.
Ver solução completa2.3) Considere um capacitor esférico preenchido com um dielétrico de constante dielétrica
e resistividade . Mostre que , onde é a resistência elétrica, é a capacitância
e a permissividade do vácuo.
Ver solução completa2.4) O valor finito da resistividade elétrica dos dielétricos utilizados nos capacitores resulta
em correntes não nulas entre as placas do capacitor, denominadas correntes de fuga. Considere um capacitor de placas planas paralelas preenchido com um dielétrico de constante
dielétrica e resistividade . Uma figura de mérito do capacitor é o produto , denominado constante de tempo, onde é a resistência elétrica e é a capacitância.
(a) Através de uma análise dimensional, mostre que possui dimensão de tempo.
Ver solução completa2.4) O valor finito da resistividade elétrica dos dielétricos utilizados nos capacitores resulta
em correntes não nulas entre as placas do capacitor, denominadas correntes de fuga. Considere um capacitor de placas planas paralelas preenchido com um dielétrico de constante
dielétrica e resistividade . Uma figura de mérito do capacitor é o produto , denominado constante de tempo, onde é a resistência elétrica e é a capacitância.
(b) Mostre que, se o capacitor estiver carregado com carga , a corrente de fuga será igual
a .
Ver solução completa2.4) O valor finito da resistividade elétrica dos dielétricos utilizados nos capacitores resulta
em correntes não nulas entre as placas do capacitor, denominadas correntes de fuga. Considere um capacitor de placas planas paralelas preenchido com um dielétrico de constante
dielétrica e resistividade . Uma figura de mérito do capacitor é o produto , denominado constante de tempo, onde é a resistência elétrica e é a capacitância.
(c) Mostre que .
Ver solução completa2.5) Considere a figura abaixo, onde um íon positivo de massa e carga possui uma
velocidade em uma região onde há um campo magnético entrando no papel.
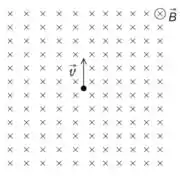
(a) Desenhe a trajetória do íon na figura.
Ver solução completa2.5) Considere a figura abaixo, onde um íon positivo de massa e carga possui uma
velocidade em uma região onde há um campo magnético entrando no papel.
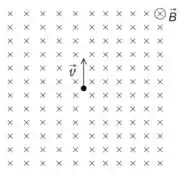
(b) Determine o raio da trajetória.
Ver solução completa2.6) Considere um toróide de raio interno e raio externo . Sabendo que o toróide possui
espiras, e que por elas circula uma corrente , calcule o campo magnético no interior do
toróide, em um ponto a uma distância do seu centro.
Ver solução completa2.7) Considere um fio cilíndrico longo de raio conduzindo uma corrente distribuída uniformemente ao longo de sua secção transversal. Determine a dependência do módulo do
vetor campo magnético com a distância medida a partir do eixo central do fio.
Ver solução completa2.8) Considere um cilindro oco de raio interno , raio externo e comprimento . O cilindro,
feito de material isolante, possui uma densidade de carga uniformemente distribuída em
seu corpo. Calcule o momento de dipolo magnético gerado pela rotação desse cilindro em torno do seu eixo longitudinal. Considere que o cilindro gira com frequência angular .
Ver solução completa2.9) Um cilindro fino de comprimento gira com frequência angular em torno de um eixo
transversal que atravessa o ponto médio entre as suas extremidades. O cilindro é feito de
material isolante e possui uma densidade linear de carga uniformemente distribuída ao
longo de sua extensão. Calcule o momento de dipolo magnético gerado pela rotação.
Ver solução completa2.10) Considere um fio cilíndrico infinito de raio conduzindo uma corrente distribuída
uniformemente ao longo da seção transversal. Quais são as duas distâncias ao eixo do fio
para as quais a intensidade do campo magnético, devido à corrente, é igual à metade do
valor na superfície?
Ver solução completa2.11) Considere um solenoide com espiras por unidade de comprimento conduzindo uma
corrente . Utilizando a lei de Ampére , determine o valor do produto
para o qual a intensidade do campo magnético gerado no interior do solenoide seja igual a . Dado: .
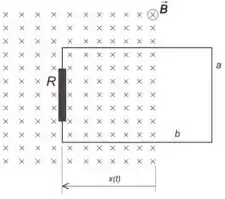
Ver solução completa3.1) Um anel retangular de largura e comprimento , contendo uma resistência , tem
seu plano orientado paralelamente ao plano do papel. Este anel é inicialmente atravessado
perpendicularmente por um campo magnético entrando no plano do papel, ao longo de
toda sua área. O campo é uniforme e de módulo constante . O anel move-se para fora
da região do campo, na direção paralela ao plano do papel, no sentido para a direita, como
indicado na figura abaixo. Sabendo que o deslocamento (veja figura) varia com o tempo
na forma , determine:
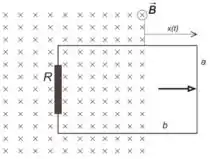
(a) O sentido da corrente induzida no anel (horário ou anti-horário de acordo com a figura).
Ver solução completa3.1) Um anel retangular de largura e comprimento , contendo uma resistência , tem
seu plano orientado paralelamente ao plano do papel. Este anel é inicialmente atravessado
perpendicularmente por um campo magnético entrando no plano do papel, ao longo de
toda sua área. O campo é uniforme e de módulo constante . O anel move-se para fora
da região do campo, na direção paralela ao plano do papel, no sentido para a direita, como
indicado na figura abaixo. Sabendo que o deslocamento (veja figura) varia com o tempo
na forma , determine:
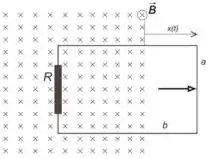
(b) A força eletromotriz induzida no anel em função do tempo .
Ver solução completa3.1) Um anel retangular de largura e comprimento , contendo uma resistência , tem
seu plano orientado paralelamente ao plano do papel. Este anel é inicialmente atravessado
perpendicularmente por um campo magnético entrando no plano do papel, ao longo de
toda sua área. O campo é uniforme e de módulo constante . O anel move-se para fora
da região do campo, na direção paralela ao plano do papel, no sentido para a direita, como
indicado na figura abaixo. Sabendo que o deslocamento (veja figura) varia com o tempo
na forma , determine:
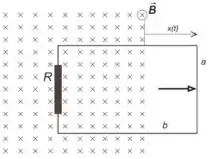
(c) A quantidade de calor dissipada pelo resistor por intervalo de tempo.
Ver solução completa3.2) Um anel retangular de largura e comprimento , contendo uma resistência , está
orientado com seu plano ortogonal a um campo magnético entrando no plano do papel.
O campo é uniforme e de módulo constante . O anel move-se para dentro da região do campo, na direção paralela ao plano do papel, no sentido para a esquerda, como indicado na
figura do problema. Sabendo que o deslocamento (veja figura abaixo) varia com o tempo
como , determine:
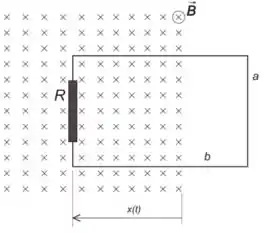
(a) O sentido da corrente induzida no anel (horário ou anti-horário de acordo com a figura).
Ver solução completa3.2) Um anel retangular de largura e comprimento , contendo uma resistência , está
orientado com seu plano ortogonal a um campo magnético entrando no plano do papel.
O campo é uniforme e de módulo constante . O anel move-se para dentro da região do campo, na direção paralela ao plano do papel, no sentido para a esquerda, como indicado na
figura do problema. Sabendo que o deslocamento (veja figura abaixo) varia com o tempo
como , determine:
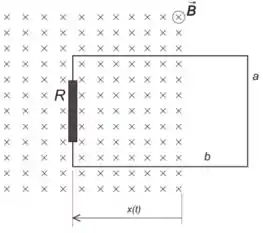
(b) O valor da corrente induzida no anel em função do tempo .
Ver solução completa3.2) Um anel retangular de largura e comprimento , contendo uma resistência , está
orientado com seu plano ortogonal a um campo magnético entrando no plano do papel.
O campo é uniforme e de módulo constante . O anel move-se para dentro da região do campo, na direção paralela ao plano do papel, no sentido para a esquerda, como indicado na
figura do problema. Sabendo que o deslocamento (veja figura abaixo) varia com o tempo
como , determine:
(c) A quantidade de calor dissipada pelo anel em um intervalo de tempo .
Ver solução completa3.3) Uma bobina de espiras, raio , resistência R, e comprimento é coaxial com
outra bobina de mesmo comprimento , mas com espiras e raio . Através da
bobina passa uma corrente que varia com o tempo como . Calcule:
(a) A corrente induzida na bobina em um instante .
Ver solução completa3.3) Uma bobina de espiras, raio , resistência R, e comprimento é coaxial com
outra bobina de mesmo comprimento , mas com espiras e raio . Através da
bobina passa uma corrente que varia com o tempo como . Calcule:
(b) A energia dissipada na bobina no intervalo de tempo entre e .
Ver solução completa3.4) Uma bobina de espiras, raio , resistência , e comprimento é coaxial com
outra bobina de mesmo comprimento , mas com espiras e raio . Através da bobina passa uma corrente que varia com o tempo como . Calcule:
(a) A força eletromotriz induzida na bobina em função do tempo.
Ver solução completa3.4) Uma bobina de espiras, raio , resistência , e comprimento é coaxial com
outra bobina de mesmo comprimento , mas com espiras e raio . Através da bobina passa uma corrente que varia com o tempo como . Calcule:
(b) A taxa com a qual a energia é dissipada na bobina , em função do tempo.
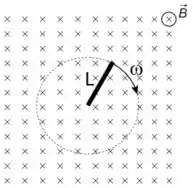
Ver solução completa3.5) Uma barra metálica de comprimento ocupa uma região onde há um campo magnético
uniforme e estático . A barra gira com velocidade angular em torno de um ponto fixo
em uma das suas extremidades, em um plano perpendicular ao campo (ver figura). Calcule
a força eletromotriz induzida na barra.
3.6) Uma barra de comprimento está orientada em direção perpendicular a um fio longo
no qual corre uma corrente . A extremidade da barra mais próxima ao fio está a uma
distância do fio e move-se com velocidade paralela ao fio (ver figura). Calcule a diferença
de potencial entre as extremidades da barra.

3.7) Um solenoide longo de raio cria um campo magnético homogêneo em seu interior, o qual varia no tempo na forma , onde é uma constante. Calcule a intensidade do
campo elétrico induzido a uma distância do eixo do solenoide e desenhe as linhas de força
do campo elétrico induzido.
Ver solução completa3.8) Um fio metálico cilíndrico de raio é envolvido por uma capa metálica cilíndrica de raio
. Um plástico isolante e não magnético preenche o espaço entre o fio e a capa (podemos
tratá-lo como vácuo). Uma corrente de mesma intensidade se propaga no fio e na capa
em sentidos opostos. Calcule a autoindutância por unidade de comprimento do cabo.
Ver solução completa3.9) O campo elétrico em uma certa região do espaço é uniforme e oscila no tempo na forma
. Determine:
(a) A densidade de corrente de deslocamento .
Ver solução completa3.9) O campo elétrico em uma certa região do espaço é uniforme e oscila no tempo na forma
. Determine:
(b) O valor máximo da corrente de deslocamento através de uma área circular de raio ,
perpendicular ao campo.
Ver solução completa3.10) Seja um capacitor de placas paralelas e circulares com raio e distância entre as placas
. Considere que há vácuo entre as placas, e que se estabeleça uma voltagem entre elas que
varia no tempo com a forma . Calcule:
(a) A densidade de corrente de deslocamento na região entre as placas.
Ver solução completa3.10) Seja um capacitor de placas paralelas e circulares com raio e distância entre as placas
. Considere que há vácuo entre as placas, e que se estabeleça uma voltagem entre elas que
varia no tempo com a forma . Calcule:
(b) O valor máximo atingido pelo campo magnético induzido.
Ver solução completa