UFMG, Sem Campus, Fundamentos de Eletromagnetismo, Listas de Eletromagnetismo - UFMG - Lista de Fundamentos de Eletromagnetismo, Questão 3.7
3.7) Um solenoide longo de raio cria um campo magnético homogêneo em seu interior, o qual varia no tempo na forma , onde é uma constante. Calcule a intensidade do
campo elétrico induzido a uma distância do eixo do solenoide e desenhe as linhas de força
do campo elétrico induzido.
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nessa questão temos um solenoide de raio que produz um campo magnético variável . Nossa tarefa é obter o campo elétrico a qualquer distância do eixo central do solenoide e também desenhar as linhas de campo elétrico induzido.
Como vamos fazer isso? 🤔
Para nos ajudar nesse problema, podemos aplicar a lei de Faraday para campos elétricos e magnéticos...
Podemos incluir o campo magnético nessa equação a partir do fluxo que é dado por
Resultando em
Legal, né? 😁
Passo 2
Vamos ter que separar o campo em duas partes, primeiro quando e depois como , isso porque o comportamento do campo �� completamente diferente em cada um dos casos.
Vamos começar para .
não depende da área, portanto podemos tirá-lo da integral assim como
Assim, a integral seria a área da circunferência de raio qualquer e o comprimento dessa circunferência.
Simplificando e substituindo por ...
Entendeu essa parte? 👀
Passo 3
Agora vamos fazer o mesmo para
A diferença é que agora terá o raio enquanto terá o mesmo raio já que fora do solenoide o campo magnético é nulo.
Simplificando e substituindo novamente...
E por fim, desenhando as linhas de campo elétrico do sistema, temos que como e seguem a regra da mão direita, então o campo elétrico aponta para a espira.
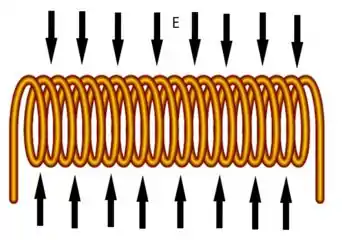
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí