UFMG, Sem Campus, Fundamentos de Eletromagnetismo, Listas de Eletromagnetismo - UFMG - Lista de Fundamentos de Eletromagnetismo, Questão 1.3
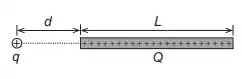
Uma carga pontual positiva está posicionada a uma distância da ponta de um bastão de comprimento com carga positiva uniformemente distribuída ao longo de toda sua extensão, conforme mostrado na figura abaixo. Calcule o módulo da força de repulsão exercida sobre a carga .
Passo 1
E aí galerinha do bem, como é que vocês estão?
Nessa questão temos um bastão de comprimento e com uma carga uniformemente distribuída, próximo a uma carguinha pontual , igual mostrado na imagem.
Queremos calcular o módulo da força de repulsão que o bastão exerce na carga .
O grande problema aqui é que o bastão é um corpo extenso, então a sua distância até a carga pontual está mudando. E aí, qual a distância que a gente coloca pra calcular a força?
Então galera, quando a distância fica variando dessa forma é interessante dividirmos o nosso corpo extenso em vários elementos pequeninhos de carga . Daí, nós podemos calcular a força que cada um desses elementos exerce na carga pontual e depois é só integrar!!!
Sacaram? Vamo nessa!
Passo 2
Bom, vamos começar calculando a força
Vamos considerar um elemento de carga que está posicionado a uma distância da extremidade do bastão mais próxima da carga . Assim, pela lei de Coulomb, vale que:
Massa! Mas, como a carga está uniformemente distribuída, podemos dizer que:
Substituindo:
Agora é só integrar dos dois lados, com variando de até . Temos:
Nossa missão se resumiu a calcular essa integral 😊
Passo 3
Temos a integral:
Fazendo a seguinte mudança de variável:
temos:
Ajeitando os limites de integração e substituindo na integral vem que:
Logo:
Portanto, a força exercida sobre a carga pontual vale:
Aeeeee! Matamos mais uma questão!
Curtiram? Responde Aí!