UFMG, Sem Campus, Fundamentos de Eletromagnetismo, Listas de Eletromagnetismo - UFMG - Lista de Fundamentos de Eletromagnetismo, Questão 3.2c
3.2) Um anel retangular de largura e comprimento , contendo uma resistência , está
orientado com seu plano ortogonal a um campo magnético entrando no plano do papel.
O campo é uniforme e de módulo constante . O anel move-se para dentro da região do campo, na direção paralela ao plano do papel, no sentido para a esquerda, como indicado na
figura do problema. Sabendo que o deslocamento (veja figura abaixo) varia com o tempo
como , determine:
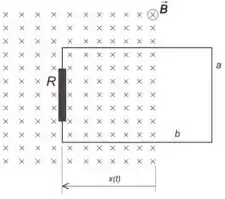
(c) A quantidade de calor dissipada pelo anel em um intervalo de tempo .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema queremos obter a potência dissipada pelo resistor ligado no circuito como mostra a figura do enunciado.
Parece tranquilo né? 😊
Pela imagem do circuito, vemos que ele está parcialmente mergulhado em um campo magnético e se movimenta horizontalmente para dentro do campo.
O que está gerando energia no circuito é o campo magnético que gera corrente e tensão induzida através da lei de Faraday.
Mas o que isso tem a ver com a potência no resistor? Veja só! 😁
Passo 2
Anteriormente vimos que a corrente e a tensão induzida no circuito pela lei de Faraday variavam com o tempo seguindo as equações
E sabemos que a potência de um resistor é dada pelo produto entre a tensão e a corrente nele, não é?
Analogamente temos que , portanto a potência dissipada pelo resistor é dada como
Bacana, não é? 😁
Passo 3
Porém, queremos saber a potência dissipada em um intervalo de tempo , então o que temos que fazer é integrar com relação a entre e
Tirando as constantes da integral, temos que
Integrando pelo método de substituição
Substituindo em
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
