UFMG, Sem Campus, Fundamentos de Eletromagnetismo, Listas de Eletromagnetismo - UFMG - Lista de Fundamentos de Eletromagnetismo, Questão 2.11
2.11) Considere um solenoide com espiras por unidade de comprimento conduzindo uma
corrente . Utilizando a lei de Ampére , determine o valor do produto
para o qual a intensidade do campo magnético gerado no interior do solenoide seja igual a . Dado: .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema, temos que obter o valor do produto onde é a corrente de um solenoide e é o número de espiras de um solenoide que produz um campo .
Tem ideia do que podemos fazer? 🤔
Pela lei de Ampere, sabemos que
Então se descobrirmos uma região que possa ser integrada para envolver o solenoide podemos obter o que estamos procurando.
Sacou? Bora começar! 😊
Passo 2
Definindo uma região de comprimento qualquer que envolva as espiras do solenoide, como por exemplo
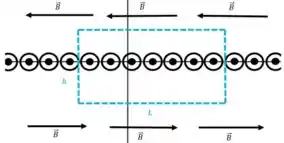
Portanto a integral de é igual a , ou seja
Já a corrente envolvida nada mais é que o número de fios dentro de (que o produto dessa linha com o número de espiras ) e da corrente do solenoide
Substituindo na lei de Ampere, temos
Isolando o produto em um lado da equação...
Então, para produzir um campo o produto entre a corrente do solenoide e o número de espiras deve ser igual a
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
