UFMG, Sem Campus, Fundamentos de Eletromagnetismo, Listas de Eletromagnetismo - UFMG - Lista de Fundamentos de Eletromagnetismo, Questão 1.2
Um fio infinito com densidade linear de carga positiva está posicionado a uma distância da ponta de um bastão de comprimento com carga positiva uniformemente distribuída ao longo de toda sua extensão, conforme mostrado na figura abaixo. Calcule o módulo da força de repulsão exercida sobre o bastão.
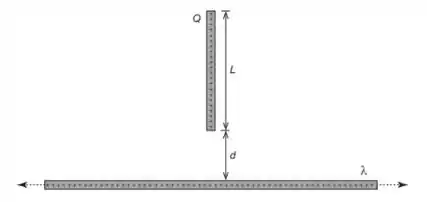
Passo 1
Oii gente, tudo bom com vocês?
Nessa questão temos um problema bem interessante!! Um fio de comprimento infinito é colocado a uma distância da ponta de um bastão. Sendo assim, o fio exerce uma força elétrica no bastão, e vice-versa.
Precisamos calcular o módulo da força elétrica resultante no bastão.
“Puts, mas a distância entre o fio e o bastão está variando...Além disso, qual o campo elétrico causado pelo fio? Como calculamos tudo isso? Socoorroo”
Calminha pessoal! Vamos por partes!!
Primeiro, pra calcular o campo elétrico do fio de comprimento infinito podemos usar a lei de Gauss. Segundo ela:
E, depois que calcularmos o campo, podemos dividir o bastão em vários pedacinhos de tamanho e calculamos a força que o fio faz em cada um desses pedacinhos e depois integramos. Tranquilo?
Vamo nessa!
Passo 2
Bom, vamos começar calculando o campo realizado pelo fio.
Traçando uma superfície gaussiana cilíndrica com raio da tampa e comprimento , temos:
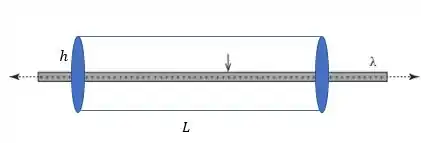
Daí, pela simetria do fio infinito, o campo aponta sempre na vertical. Por isso, o produto escalar:
será nulo nas tampas do cilindro, pois aí os vetores serão perpendiculares.
Logo, pela lei de Gauss precisamos considerar apenas a superfície lateral do cilindro. Daí:
Como o fio é infinito na horizontal, o campo deve depender apenas da altura até o fio. Então, ele não varia na superfície lateral e podemos colocá-lo para fora na integral:
Integrando todos os elementos da superfície lateral do cilindro, temos justamente a área lateral do cilindro, que vale:
Já quanto à carga interna à superfície gaussiana cilíndrica, como a densidade linear vale , temos:
Daí, substituindo na equação principal:
Massa! Conseguimos calcular o módulo do campo elétrico e sabemos que ele aponta sempre pra cima na região acima do fio.
Passo 3
Agora que já temos o campo, podemos considerar que a força elétrica em um elemento em uma posição de altura a partir da extremidade inferior do bastão do bastão vale:
Mas:
E, considerando a carga uniformemente distribuída no bastão, temos também que:
Assim:
Agora sim!! Integrando de até , vemo:
Fazendo:
temos:
Ajeitando também os limites de integração, ficamos com a seguinte expressão para :
Logo:
E é issooo!! Esse é o módulo da força resultante que o fio faz no bastão!
Bem legal né? Valeu pessoal!! Até a próxima 😉