UFMG, Sem Campus, Fundamentos de Eletromagnetismo, Listas de Eletromagnetismo - UFMG - Lista de Fundamentos de Eletromagnetismo, Questão 3.1b
3.1) Um anel retangular de largura e comprimento , contendo uma resistência , tem
seu plano orientado paralelamente ao plano do papel. Este anel é inicialmente atravessado
perpendicularmente por um campo magnético entrando no plano do papel, ao longo de
toda sua área. O campo é uniforme e de módulo constante . O anel move-se para fora
da região do campo, na direção paralela ao plano do papel, no sentido para a direita, como
indicado na figura abaixo. Sabendo que o deslocamento (veja figura) varia com o tempo
na forma , determine:
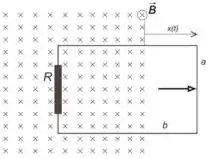
(b) A força eletromotriz induzida no anel em função do tempo .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema temos que obter a tensão induzida no circuito que está mergulhado em um campo magnético como podemos ver na imagem do problema.
Tem ideia de como fazemos isso? 🤔
Segundo a lei de Faraday, a tensão induzida em um circuito é igual a variação do fluxo magnético que passa por ele.
Mas podemos relacionar o fluxo como onde é o campo magnético e é a área do circuito.
Podemos começar agora? 👀
Passo 2
Descobrimos que a tensão induzida é igual a multiplicada pela variação da área.
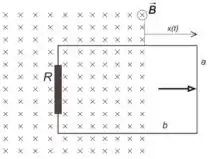
Analisando o circuito, temos que a área é dada pelo retângulo de altura e largura
Ou seja
Substituindo em ...
Como , então
Como é constante em relação a , a derivada desse termo é igual a , mas derivando com relação a pelo método de derivação polinomial, temos
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
