UFMG, Sem Campus, Fundamentos de Eletromagnetismo, Listas de Eletromagnetismo - UFMG - Lista de Fundamentos de Eletromagnetismo, Questão 3.2b
3.2) Um anel retangular de largura e comprimento , contendo uma resistência , está
orientado com seu plano ortogonal a um campo magnético entrando no plano do papel.
O campo é uniforme e de módulo constante . O anel move-se para dentro da região do campo, na direção paralela ao plano do papel, no sentido para a esquerda, como indicado na
figura do problema. Sabendo que o deslocamento (veja figura abaixo) varia com o tempo
como , determine:
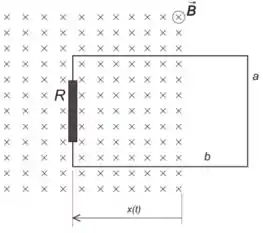
(b) O valor da corrente induzida no anel em função do tempo .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema temos que obter a corrente induzida no circuito que está mergulhado em um campo magnético como podemos ver na imagem do problema.
Tem ideia de como fazemos isso? 🤔
Para obter a corrente no resistor, temos antes que obter a tensão no resistor e depois aplicar a lei de Ohm
Segundo a lei de Faraday, a tensão induzida em um circuito é igual a variação do fluxo magnético que passa por ele.
Mas podemos relacionar o fluxo como onde é o campo magnético e é a área do circuito.
Podemos começar agora? 👀
Passo 2
Descobrimos que a tensão induzida é igual a multiplicada pela variação da área.
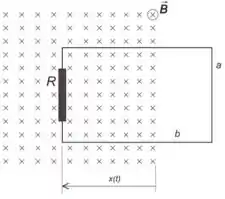
Analisando o circuito, temos que a área é dada pelo retângulo de altura e largura
Ou seja
Substituindo em ...
Como , então
Como e são constantes em relação a , a derivada desses termos são iguais a , mas derivando com relação a pelo teorema fundamental do cálculo, temos
Tranquilo até aqui? 😐
Passo 3
O sinal é apenas uma referência da polaridade da tensão, então podemos considerar a tensão apenas como
Agora, pela lei de Ohm, temos que a corrente que passa pelo resistor é dado por
Analogamente, temos que , ou seja
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
