(Capítulo 14.7 – Exercício 29) Determine os valores máximo e mínimo absolutos de no conjunto .
, é a região triangular fechada com vértices , e .
Passo 1
E aíí gente, vamos lá? O problema pede para encontrarmos os extremos absolutos de no conjunto . Como é contínua e é fechado e limitado, o teorema do valor extremo garante que a função tem máximo e mínimo global nesse conjunto, certo?
Os candidatos a extremos globais serão os pontos críticos de no interior de junto com os valores extremos de na fronteira de .
Neste caso, é o triangulo desenhado a seguir:
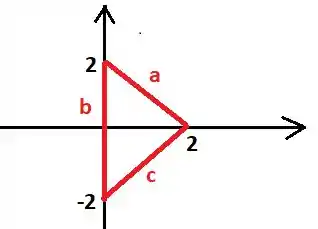
Então vamos lá
Passo 2
A fronteira é dividida em três partes:
Vamos encontrar os pontos críticos de :
Assim, o único ponto crítico de é . Note que esse ponto está no interior de . Ele é um dos candidatos a extremos absoluto!
Passo 3
Agora vamos olhar para a fronteira de . Primeiro para , em que . Substituindo essa relação na expressão para , obtemos uma função de uma variável apenas:
Assim,
Sabemos que está restrita ao intervalo . Um possível candidato a extremo dessa função é obtido fazendo :
Assim, um novo candidato a extremo de é o ponto .
Na parte , , de modo que
Assim, implica
Portanto, o candidato aqui é o ponto
Por fim, na fronteira com :
Assim, o ponto crítico é e o candidato a extremo de é .
Já temos então quatro candidatos a extremos absolutos de . Mas ainda falta considerar os extremos das fronteiras: as pontas do triângulo! Assim, todos os candidatos a extremos globais são:
Passo 4
O que temos que fazer agora é avaliar o valor da função em cada um desses pontos:
Desta forma, o mínimo absoluto ocorre em enquanto o máximo ocorre em e .
E acabaaamos, ufa!