Sejam dada por e
1. Determine todos os pontos críticos de em .
2. Classifique todos os pontos críticos de em .
3. Determine os pontos de máximo e mínimo de na circunferência
4. Determine os pontos de máximo e mínimo de em .
Passo 1
Salve galera! Vamos lá resolver essa questão. Para o primeiro item, precisamos descobrir os pontos críticos de dentro da região dada. Vocês sabem a formula padrão para pontos críticos em funções de 2 variáveis?
Isso significa que:
Dessa forma, podemos montar um sistema que relaciona as duas partes da equação:
Logo:
Portanto, os pontos críticos para a função vão ser justamente as combinações dos pontos para:
Portanto, os 4 pontos críticos vão ser:
Belezura, item 1 feito. Bora pro próximo?!
Passo 2
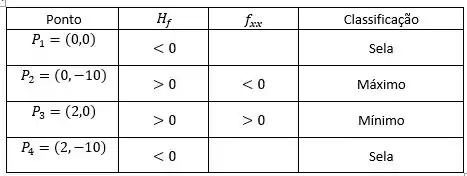
Aqui no item 2, precisamos classificar esses pontos. Temos as classificações, para os pontos críticos, divididos em: Máximos, mínimos e pontos de selas. A gente descobre isso através de uma relação entre a segunda derivada e o determinante Hessiano. Então, resolvendo por partes. Primeiro pra segunda derivada, temos que:
Agora, para o Hessiano, vocês lembram como ele é descrito? Ele é dado por:
Desenvolvendo:
Show. Agora que temos os valores de cada segunda variável, podemos classificar de acordo com a seguinte forma: Se , então o ponto automaticamente é sela. Se , então vamos para o teste da segunda derivada. Para e , temos um ponto de mínimo. Para e , temos um ponto de máximo. Achamos essa relação simplesmente aplicando os valores de e que achamos em cada ponto. Agora é hora de classificar:
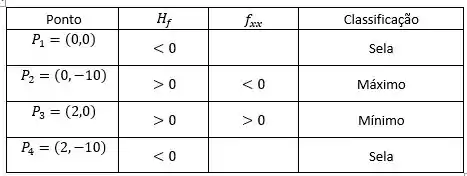
Passo 3
Showzinho. Agora a questão pede pra gente achar os pontos de máximo e mínimo para uma nova função
Isso meio que “limita” a área aonde os pontos de máximo e mínimo devem ser contidos. Qual o método mais otimizado pra gente resolver esse tipo de problema? Isso mesmo, o método dos multiplicadores de Lagrange. Através desse método, achamos os pontos de máximo e mínimo da função, através do seguinte sistema:
Aplicando para as nossas funções:
Logo,
Portanto, aplicando para o nosso sistema de multiplicadores de Lagrange:
Logo,
Passo 4
Dessa forma, nosso sistema pode ser reescrito como:
Sisteminha com 3 incógnitas e três equações não lineares. Para resolver esse sistema, vamos dividir todos os casos possíveis em que , e por fim .
Para , pela equação de restrição :
Gerando os pontos:
Para , pela equação de restrição :
Gerando os pontos:
Passo 5
Para os casos em que: , temos o seguinte sistema:
Substituindo e na terceira equação, temos que:
Dessa forma:
Aplicando na primeira equação:
Aplicando isso na segunda equação:
Portanto, todos os pontos que satisfazem o sistema de equação são:
Agora precisamos tabelar isso e saber quem são os pontos que aplicados na função, vão nos retornar o maior valor e o mínimo valor de . Esses pontos vão ser justamente os pontos de máximo e mínimo, respectivamente. Logo, aplicando em uma tabela:
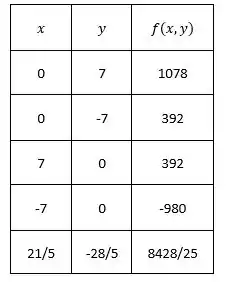
Podemos perceber que o ponto de máxima é:
E o ponto de mínima é:
Passo 6
Belezinha, agora no item 4, vamos definir os pontos de máxima e mínima dentro do domínio . E esses pontos são constituídos ou pelos pontos de máximo de mínimo de , que estão contidos em . Como também pelos valores de máximo e mínimo na fronteira de (que calculamos no item 3). Pra gente visualizar melhor, vamos considerar essa região como:
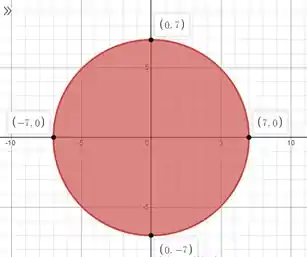
Os pontos marcados na região são os pontos obtidos no item e no item . Contudo, nem todos os pontos que achamos lá no item estão representados, pois não pertencem a e portanto, não são de interesse. Para estes pontos, encontramos então, tabelados:
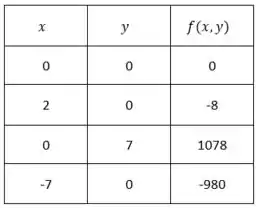
Logo, os máximos e mínimos correspondem aos mesmos do item passado:
E é isso! WE DID IT!!! Se ficou alguma dúvida, quer dar alguma sugestão ou reportar algum erro, manda um feedback pra gente! Vamos adorar ajudar você
Resposta
1-
2-
3
O ponto de máxima é:
E o ponto de mínima é:
4- Mesmos pontos do item 3.