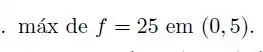Passo 1
Primeiramente, queremos valor máximo, então vamos começar calculando os pontos críticos e depois a gente vê o que dá pra fazer.
Calculando as derivadas parciais:
Se igualarmos isso a zero, teremos uma inverdade, certo?
Isso significa que a função não tem pontos críticos, assim, os pontos de máximo devem ocorrer nos vértices da região restrição.
Passo 2
Beleza, então vamos seguir a sugestão da questão e desenhar as restrições de .
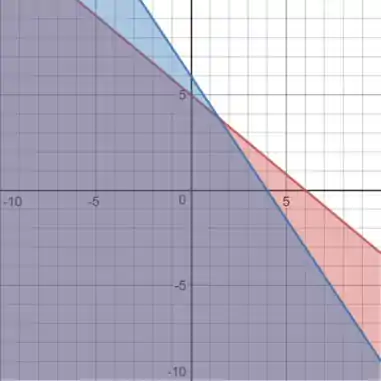
A reta vermelha é a reta
E a reta azul é a reta
Agora tem também as restrições de e .
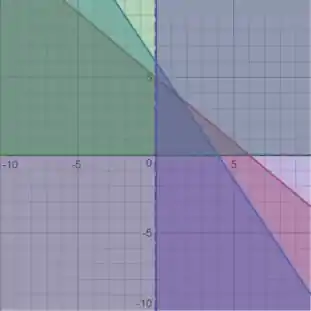
Assim, nossa região de restrição será o polígono em destaque:
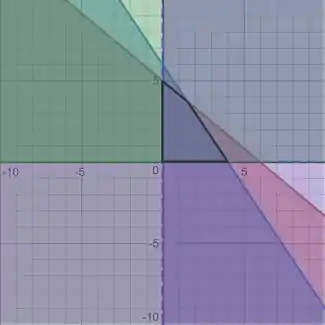
Agora, vamos para as curvas de nível de . Para , temos:
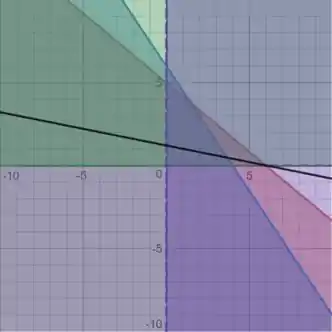
Para outros valores crescendo, temos:
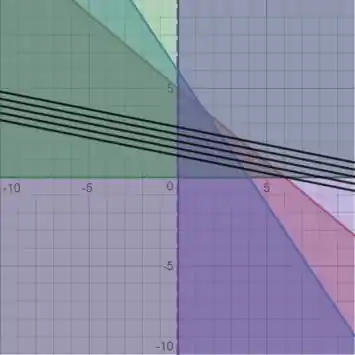
Passo 3
Ou seja, cresce quando se aproxima do vértice superior do polígono de restrição. Esse vértice superior é justamente o ponto , em que:
Resposta