Encontre o maior e o menor valor de no círculo . Em que pontos tais valores são atingidos?
Passo 1
Bom pessoal, nessa questão aí a gente tem que achar os máximos da função só em um intervalo específico: um círculo de raio :
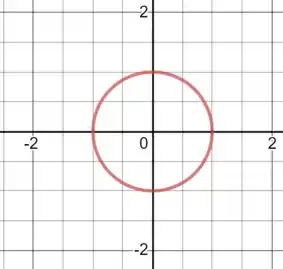
Nesse tipo de problema, você precisa lembrar de dois passos: primeiro encontrar os pontos críticos no interior do círculo, e segundo encontrar os valores máximos e mínimos na borda do círculo.
Passo 2
Vamos começar procurando os pontos críticos no interior do círculo. Pra isso a gente precisa tirar as derivadas parciais em relação a e :
E um ponto é crítico quando essas duas derivadas são iguais a zero sobre ele. Então ficamos com um sistema:
Multiplicando a equação de baixo por :
E agora somando as duas:
E substituindo na primeira equação:
Ou seja, é um ponto crítico. E nesse caso:
Ok, vamos guardar essa informação.
Passo 3
Agora a gente tem que olhar pra borda do círculo, e procurar o maior e o menor valor.
Isso é diferente de procurar o ponto crítico, aqui só queremos achar o máximo e o mínimo nessa borda.
Aqui pode ser uma boa escrever o problema em coordenadas polares. A transformação é essa aqui:
E já que a gente só quer olhar a borda do círculo, vamos fixar , então:
Então a função tem a seguinte forma quando estamos na borda:
E como :
Mas ainda não é óbvio qual vai ser o valor de que dá o maior e o menor valor da equação.
Vamos então usar essa identidade aqui:
Ou seja:
Passo 4
Tá, qual é o maior valor que essa função aqui assume?
O valor máximo de vai aparecer quando , certo? E como , então:
O valor mínimo de vai aparecer quando , que é o caso do , então:
E quais os valores de nesses casos?
E quais são as coordenadas e nesses pontos?
O que na prática, significa que se é par, temos os pontos:
E se é ímpar, temos os pontos:
Passo 5
Ok pessoal. Então a gente localizou cinco candidatos a máximo e mínimo do círculo:
Então o valor máximo da função no círculo é simplesmente o maior desses três valores, ou seja:
E o valor mínimo é o menor dos três:
Pronto, resolvido!
Resposta
O maior valor é , que ocorre no ponto . O valor mínimo é , que ocorre no ponto .