Determine os valores máximo e mínimo absolutos de
no conjunto
Passo 1
Antes de mais nada, é bom visualizar o conjunto . E nesse caso, até que é bem simples: temos e . Então e . vai ser um quadrado:
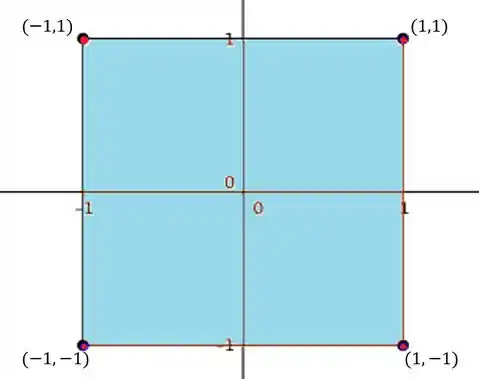
Dito isso, podemos continuar :)
Passo 2
Essa é uma questão de máximos e mínimos, então o nosso primeiro reflexo tem que ser: achar as derivadas parciais de e igualá-las a para achar os pontos críticos de . Então vamos lá:
Logo:
Agora igualando a :
- Se , como então ; o que nos dá o ponto .
- Se então ; o que nos dá os pontos .
Mas repare que esses dois últimos pontos não pertencem ao quadrado . Logo, o único ponto crítico de em é .
Passo 3
Agora vamos dar uma olhada na fronteira do quadrado. Podemos notar que os vértices do quadrado são candidatos a máximo e mínimo, pois eles são os extremos da região. Isso nos dá mais 4 candidatos: os pontos , , e .
Vamos analisar agora os lados do quadrado um por um. Repare que vamos sempre ter uma coordenada variando de -1 a 1 enquanto outra fica fixada. Ou seja, na borda do quadrado a só depende de uma variável.
Por isso, pra facilitar nossa conta, vamos criar uma função de uma variável para cada lado e determinar os pontos críticos dessas funções. Esses pontos críticos também vão ser candidatos a máximo ou mínimo da no quadrado. Ficou confuso? Relaxa que não é tão complicado, dá uma olhada:

Passo 4
Lado 1: e
tem um ponto crítico: o ponto , que é, portanto, mais um candidato a ponto de máximo ou mínimo.
Lado 2: e
Assim, obtemos mais um candidato, o ponto .
Lado 3: e
A função é consante então para todo vamos ter .
Então, o lado 3 todo é candidato a conter o valor máximo ou mínimo de no quadrado. Já tínhamos considerado como candidatos os vértices e . Mas agora podemos considerar todos os pontos , com , beleza?
Lado 4: e
Repare que . Então, que nem pra , vamos ter que o ponto crítico de tem . Mas agora . Isso nos dá mais um candidato, o ponto .
Passo 5
Show! Achamos todos os candidatos a ponto de máximo ou mínimo de no quadrado, são os pontos:
Agora "só" nos resta calcular o valor da em cada ponto e ver qual vai ser o máximo e qual vai ser o mínimo! Lembrando que , vamos ter:
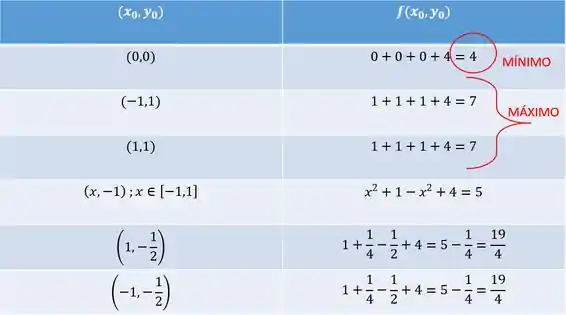
Comparando os valores, podemos ver que o valor mínimo é , no ponto , enquanto o valor máximo é , nos pontos e .
Resposta
Máximo: , nos pontos e
Mínimo: , no ponto .