Seja dada por

1. Determine os pontos críticos de e classifique-os.
2. Determine, se houver, os pontos de máximo e mínimo de restrita ao conjunto

Da primeira equação:

Assim

Ou

Se , a segunda equação do sistema fica

Ou

E temos os pontos

Agora, se , a segunda equação nos diz que

E temos os pontos

Vamos analisar que tipos de pontos críticos são estes. Para isso, vamos calcular as derivadas segundas:

Agora vamos ao teste da derivada segunda.

Vamos calcular num ponto genérico pra facilitar nossas vidas e depois a gente testa os pontos, já que temos muitos pontos.

Beleza, agora vamos analisar o sinal desse determinante para cada um dos pontos críticos.

Começando por :

Então é um ponto de sela.

Vamos testar o ponto :

Então também é um ponto de sela.

Agora vamos ver os pontos :

Beleza, então podemos ter pontos de máximo ou mínimo local.

Vamos analisar o sinal de em cada um desses pontos:

Assim, é ponto de mínimo local e é ponto de máximo local.

Para encontrar os pontos de máximo e mínimo globais de uma função com restrição o processo é sempre o mesmo: Verificar se há um ponto crítico dentro da região, e verificar se há máximos e mínimos na fronteira da região.

Os pontos críticos nós já encontramos na letra . São eles:

Vamos só verificar agora se eles estão dentro da região .

O único ponto que atende as condições de estar dentro do conjunto é o ponto Todos os outros então podem ser descartados.

Então guardamos o ponto . Também precisamos guardar os vértices da nossa região.

Desenhando nossa região, temos que ela é a parte de dentro desse triangulo:

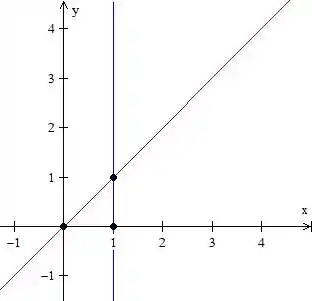
E os vértices são os pontos:

Portanto, temos mais 3 pontos candidatos a máximo e mínimo.

Agora, devemos verificar pontos de máximo ou mínimo na fronteira.

Assim, temos 3 lados a serem verificados:

Quando em que são os lados do triângulo.

Em cada lado a função só depende de uma variável, e nós temos que achar os pontos críticos dessas 3 “subfunções”.

Comecemos pelo lado . Lembrando a nossa função:

E o primeiro lado:

Substituindo o lado na função:

Assim, já temos logo que

Agora precisamos fazer o mesmo pro segundo lado :

Substituindo esse lado na função, teremos:

Temos que achar os pontos críticos dessa função, vamos derivar e igualar a zero. Neste caso derivamos em relação a

Então temos o ponto

Mas já vimos antes esse ponto como vértice da região, então o lado 2 não acrescentou nada de novo!

Vamos verificar para o terceiro lado :

Substituindo-o na função:

Neste caso derivamos em relação a

Ou

Assim, obtemos os pontos e . Mas o nós já consideramos, é um vértice do retângulo!

Então o lado 3 só acrescentou um ponto novo.

Ok, agora já temos todo o material necessário para terminar de vez com isso e dizer quais são os pontos de máximo e mínimo!

Os nossos candidatos são os pontos:

Só nos resta calcular o valor da função em cada ponto. Lembrando que

Então temos

Show, então os pontos de mínimo global e máximo global de em são, respectivamente, e .

O valor mínimo é e o valor máximo é .