Seja dada por
- Determine e classifique os pontos críticos.
- Determine , caso existam, os pontos de máximo e de mínimo de no conjunto
Passo 1
Essa é tranquila né? Você também não sente na cabeça aquela voz ressoando “deriva e iguala a zero” quando alguém te pede pra encontrar ponto crítico de uma função? Se não sente, tudo bem, isso não faz tanta diferença assim...
Mas preste atenção, aqui temos uma função de duas variáveis, isso significa que ela tem duas derivadas parciais, em relação a e em relação a . Então, o vetor gradiente, que é , que deve valer , ou seja, cada derivada parcial deve valer !
Passo 2
Sem mais enrolação, vamos derivar a função em relação a e a !
Beleza, agora sabemos o vetor gradiente:
Passo 3
Igualando o vetor gradiente a teremos:
Ou seja,
Da equação de cima, temos
Da equação de baixo, temos
Passo 4
Agora que temos os valores de e que tornam as derivadas parciais iguais a , podemos montar os pontos críticos! Sendo e , nossos pontos são:
Passo 5
Vamos agora classificar nossos pontos críticos? Para isso, fazemos o teste da segunda derivada, usando o determinantes dado por:
Bom, como o próprio nome diz, temos que calcular as segundas derivadas!
Vamos lá, para temos:
Para temos:
E para temos:
Portanto, nosso determinante fica:
Passo 6
Perfeito, agora temos tudo o que precisamos para classificarmos os pontos!
Apenas relembrando o teste da segunda derivada, se:
- é ponto de máximo ou mínimo
- é ponto de sela
- nada sabemos sobre o ponto
Se é ponto de mínimo
Se é ponto de máximo
Então, para os pontos teremos,
Como e , então é um ponto de mínimo
Como , então é um ponto de sela
Como , então é um ponto de sela
Como e , então é um ponto de máximo
Passo 7
b) Determine , caso existam, os pontos de máximo e de mínimo de no conjunto
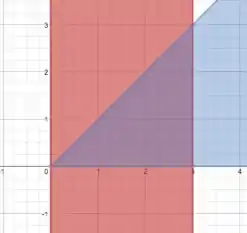
A primeira coisa a se fazer aqui, é desenhar esse domínio!
Temos variando entre e e está entre e a reta
 2
2
E aí está, é a região triangular, em roxo :)
Passo 8
E agora, o que faremos? Bom, não adianta nada saber onde está o domínio se não pudermos usá-lo de maneira prática. Então, como fazer equação cartesiana normalmente não é pratico, é melhor usarmos curvas parametrizadas e restringir o parâmetro.
Para o segmento que vai percorrendo o eixo de a (base do triângulo), teremos:
Para o segmento que faz ângulo reto com o eixo (lado direito, vertical, do triângulo), teremos:
E para o segmento que corresponde ao pedaço da reta entre a origem e o ponto , teremos:
Passo 9
Beleza, vamos agora partir pras contas ;)
A missão é percorrer a função com cada um dos segmentos, buscando possíveis candidatos a máximo e mínimo. Ou seja, vamos substituir as parametrizações na equação da função , e, depois, derivamos e igualamos a . Os valores encontrados para serão os dos pontos nos quais as derivadas valem , ou seja, máximos ou mínimos!
Não podemos esquecer que entram como candidatos, não só os pontos onde a derivada vale zero sobre os segmentos, mas também os vértices dos triângulo e possíveis pontos no seu interior (no caso dos pontos do interior, a derivada deve valer ).
Sem mais enrolação, vamos percorrer a função com a primeira curva:
Então, teremos que:
Agora derivamos...
E como a derivada deve valer ...
Como , o único valor possível é .
Com e com , temos os pontos:
OBS: Lembre-se do que falamos, apesar de apenas um ponto ser o que tem derivada igual a , os outros dois são os vértices do triângulo contidos no segmento , com um extremo com e outro em .
Passo 10
Agora, percorrendo com as segunda curva, teremos:
Então, teremos:
Agora derivamos...
E igualamos a ...
Beleza, encontramos mais um valor para o parâmetro! Com e , temos os pontos
Perceba que esse segmento também tem o ponto em uma das extremidades, mas ele já é o ponto do passo anterior!
Passo 11
Finalmente, percorremos agora a função pela terceira curva:
Com essa, teremos:
Então derivamos...
E igualamos a ...
E para e , temos o ponto
Novamente, para com entre e , teríamos os pontos e como extremos, mas esses já são os pontos e encontrados anteriormente!
Passo 12
Finalmente, agora é só pegar esse conjunto de pontos, colocar os valores de e na função e ver qual deles é o máximo e o mínimo! Ahh, e já íamos esquecer os pontos no interior! Para aqueles que tínhamos calculado no item , o único que está dentro do triângulo é o . Então, vamos escrever nosso grupo de pontos!
Agora, vamos colocar esse pontos todos na função:
Ok, vamos parar esse passo por aqui e deixar o próximo para o trabalho braçal...
Passo 13
Então, é só colocar os valores de e de cada ponto nos valores de e da equação. Vou fazer tudo de uma vez pra não adicionar mais passos nessa resolução, belê?
E aí está! Dentre todos esses pontos, temos que o mínimo é e o máximo é
Resposta
- é ponto de mínimo, e é ponto de máximo, em