UFSCAR – Cálculo 2 – Banco de Questões – Questão 16
Seja a função definida por
Onde D é a região triangular fechada com vértices . Preencha os espaços abaixo:
- O valor máximo absoluto de é :
- O valor mínimo absoluto de é:
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas estou aqui para te ajudar! Vamos resolver juntos?
O problema nos dá uma função e pede os pontos de máximo e mínimo em uma região. Bom pra fazer isso precisamos seguir os seguintes passos:
- Desenhar a região: sem o desenho desse triângulo e as funções que delimitam não vai rolar! Então, desenho nele!
- Achar os pontos críticos da função (sem envolver a restrição ainda): derivar parcialmente a função e igualar a zero. Daí deve sair algum ponto, e esse ponto a gente pode classificar entre máximo, mínimo e de sela.
- Depois disso verificar se na região de fronteira há alguma coisa: parametrizar as retas que delimitam a região , substituir na função , derivar e igualar a zero. Aí devem sair alguns pontinhos pra gente analisar.
- E com todos os pontos na mão, substituir na função e achar qual é o maior e o menor.
Beleza?
Tenso né? Mas calma, vou fazer com você. Me segue para o passo a passo!
Passo 2
Agora a região . Os vértices do triângulo delimitam nossa região. Os vértices são:
Colocando esses pontos num plano cartesiano temos a seguinte região:
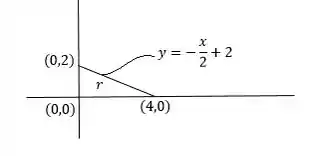
A equação da reta que passa pela hipotenusa do triângulo é:
Pra resolver essa parte é bem tranquilo: multiplica os elementos da diagonal principal (em AZUL) e os elementos da diagonal secundária (em VERMELHO E trocando o sinal):
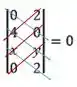
Tá, guarda essa equação da reta!
Passo 3
Agora vamos aos pontos críticos da função: derivar parcialmente e igualar cada uma a zero.
Daqui temos que o ponto é crítico. Agora vamos classificar esse bichinho.
Derivando mais uma vez pra fazer o teste da derivada segunda:
E o hessiano é:
Passo 4
Agora vamos em busca de pontos na fronteira: parametrização!
Vamos parametrizar cada segmento e ir percorrendo a função com cada um deles, buscando possíveis candidatos. A ideia aqui é: substituir a parametrização, derivar e igualar zero. Os valores de encontrados são os pontos nos quais a derivada é igual a zero e o ponto crítico.
Para a base do triângulo: , com :
Então nesse segmento não temos pontos críticos.
calma, ainda faltam outros segmentos!
Para a altura do triângulo: , com :
Então nesse segmento também não temos pontos críticos.
E agora na hipotenusa (aqui que entra aquela equação do passo 1!!! Chamando o vai ser igual aquela equação lá, é só trocar por !):
Ará! Aqui sim encontramos um ponto crítico!
Agora vamos descobrir que ponto é esse:
Então os pontos críticos são: os extremos do intervalo e dentro do triângulo e (esse último é de sela!).
Passo 5
Agora com os pontos na mão, vamos testar na função pra ver qual é maior/menor:
e
Então temos:
- , máximo absoluto
- , mínimo absoluto
- , máximo absoluto
- , mínimo absoluto
ufa! Terminamos!
Espero ter ajudado!
Resposta
Resposta
Ei, a resposta está no passo a passo :)