Encontre o máximo e o mínimo absoluto da função
na placa retangular (veja figura a seguir).
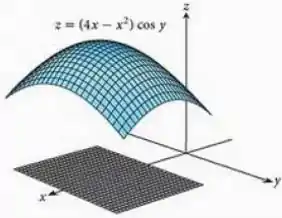
Passo 1
Vamos achar os pontos críticos da função, igualando as derivadas parciais a zero:
Temos
Passo 2
Comecemos pela derivada parcial em relação a :
Vamos ver as restrições da placa retangular:
Portanto, sem problemas pra , mas não pode!
Então concluímos que .
Passo 3
Agora zeremos a derivada parcial em relação a :
Se :
Mas como , nenhum dessas opções é válida.
Então nos sobra . Como , devemos ter .
Portanto, possui um ponto crítico nessa placa retangular: o ponto . Ele é o nosso primeiro candidato a ponto de máximo ou mínimo absoluto da função na placa.
Passo 4
Agora temos que analisar a fronteira do retângulo:
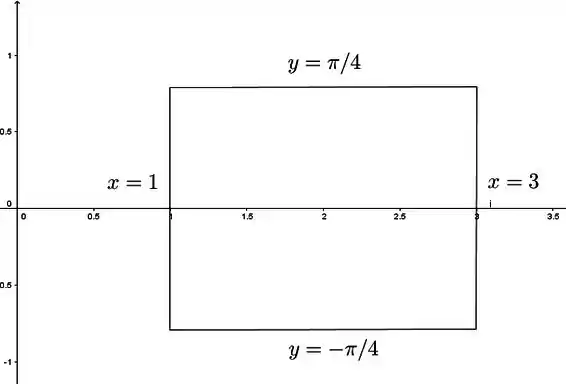
Vamos estudar os lados um por um e determinar que candidatos a ponto de máximo ou mínimo temos em cada um deles.
Passo 5
Os primeiros candidatos que podemos separar são os 4 vértices do retângulo, os pontos:
Agora sim vamos olhar os lados um por um.
Passo 6
Começando pelo lado de cima, onde
Assim, nesse lado a função passa a depender só de :
Derivando e igualando a zero:
Portanto, o ponto é mais um candidato.
Passo 7
Vejamos agora o lado da direita:
Agora a função só depende de :
Continuando:
Então achamos mais um ponto: .
Passo 8
Passamos agora pro lado de baixo:
Nesse lado, temos
Repare que a função ficou igual ao lado de cima. Da mesma forma, temos
Então encontramos mais um ponto: .
Passo 9
Enfim chegamos ao último lado, o da esquerda, onde
Aqui temos
Essa ficou igual ao lado da direita. Assim,
Achamos o último candidato: o ponto .
Passo 10
Agora só nos resta calcular o valor da função em todos esses pontos e determinar qual é o mínimo global e qual é o máximo global:

Portanto, o valor máximo de na placa retangular é , atingido no ponto .
O valor mínimo é , obtido nos pontos e .
Aliás, podemos ver que esses pontos são compatíveis com a figura.
Resposta
Máximo: , em .
Mínimo: , em e .