Questão 5 – Considere a função
a) Calcule as derivadas parciais de primeira e segunda ordem.
b) Determine os pontos de sela, de máximo e mínimo locais, se existirem, preenchendo a tabela abaixo
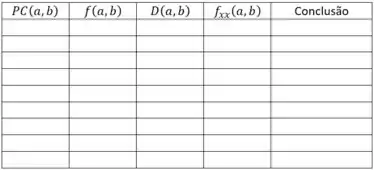
c) Determine os pontos de mínimo e máximo absolutos de na região interna delimitada (fronteira inclusa) pela curva abaixo, cuja equação é .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nessa questão, temos algumas coisas a fazer e temos que usar como instrumento a função dada por .
Primeiramente foi pedido para obter as derivadas parciais de de primeira e segunda ordem.
Depois vamos ter que obter os pontos críticos e classifica-los como pontos de máximo, mínimo ou de sela preenchendo a tabela dada no enunciado.
E por último, temos que determinar os pontos de máximo e mínimo absolutos que estão dentro da região limitada pela equação .
Haja contas, não é? 👀
Bora começar!
Passo 2
No item a) temos que calcular as derivadas parciais de primeira e segunda ordem de . No caso , , , , e
Primeiro vamos obter as derivadas parciais com relação a .
Derivando com relação a , temos
Aplicando o método de derivação polinomial
Simplificando o resultado, temos
Agora derivando com relação a vamos obter a derivada mista
Como não temos em , a derivada resulta em
Agora vamos obter a derivada de segunda ordem derivando com relação a
Pelo método de derivação polinomial, temos
Tranquilo até aqui? 😎
Passo 3
Agora vamos obter as derivadas de .
Derivando com relação a , vamos ter
Pelo método da derivação polinomial
Vamos obter a derivada mista derivando com relação a , veja só
Como também não temos para derivar aqui, o resultado é igual a
E por último, vamos obter a derivada de segunda ordem derivando com relação a de novo.
Aplicando o método de derivação polinomial
Dessa forma, obtemos todas as derivadas parciais de primeira e segunda ordem de !
Interessante, não é? 😁
Passo 4
Agora, para o item b), temos que obter os pontos críticos de e classifica-los como máximo, mínimo ou sela.
Os pontos críticos da função são obtidos igualando e a , ou seja
Simplificando esse sistema dividindo os dois lados da igualdade por , temos
Para quais valores de e que tal número elevado ao cubo é igual a ele mesmo?? 🤔🤔
No caso, temos três valores que se encaixam nessa descrição, não é?
Portando os pontos críticos serão as combinações dessas coordenadas.
, , , , , , , e por fim .
Muitos pontos, não é?? 👀👀
Na tabela, a primeira coluna é o ponto crítico que encontramos, no caso , ...
A segunda coluna diz respeito ao valor da função no ponto, ou seja, a imagem do ponto em .
A terceira coluna é o valor de onde é dado pelo determinante da matriz
Substituindo as derivadas pelas suas equações, temos
A quarta coluna é o valor do ponto aplicado na segunda derivada de com relação a
E por último, a quinta coluna é a nossa conclusão se o ponto é máximo, mínimo ou de sela.
Entendeu? Vamos começar na ordem dos pontos!
Passo 5
Para o ponto , a imagem na função resulta em
Aplicando o ponto em , temos
Aplicando o ponto na segunda derivada de com relação a
Como é maior que e é menor que , o ponto é classificado como ponto máximo!
Tranquilo até aqui? 😉
Passo 6
Agora vamos fazer o mesmo para o ponto .
Obtendo a imagem do ponto na função , temos
Aplicando em
Calculando a segunda derivada de em no ponto
Dessa forma, como foi menor que , podemos afirmar que é um ponto de sela!
Bacana, não é? 😁
Passo 7
Para o ponto .
Calculando a imagem na função
Aplicando em
E em o ponto resulta
Da mesma forma que o ponto anterior, resultou em um nomero menor que , então certamente é ponto sela!
Está acompanhando? 👀
Passo 8
Como já vimos como fazemos, podemos substituir os resultados diretamente na tabela.
Mas de forma geral, se e , o ponto é classificado como mínimo, se e , o ponto é classificado como ponto máximo e se o ponto é classificado como ponto sela.
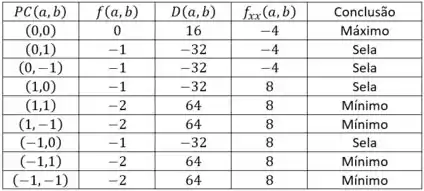
Interessante, não é? 🤩
Passo 9
Por fim, vamos obter os pontos de máximo e mínimo dentro da região limitada pela equação .
Olhando para a nossa função
Percebemos que a equação está contida na função, ou seja
A parte entre parênteses não é exatamente o lado esquerdo da equação? Então se o lado esquerdo é igual a , reescrevemos a função como
Obtendo as derivadas parciais da nova função, temos
Pelo método de derivação polinomial, vamos obter a derivada de com relação a e como não tem , a derivada com relação a é igual a .
Relaxa, estamos acabando! 😉
Passo 10
Igualando as derivadas a , temos
Assim, vemos que
Fazendo em , temos
Portanto, temos um único valor que não influencia no resultado.
Se analisarmos os pontos obtidos no item a), vemos que toso eles estão contidos dentro da região do item c).
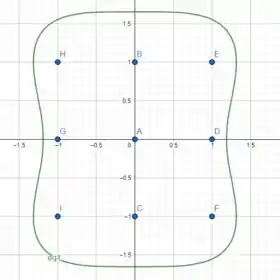
Comparando os resultados das imagens dos pontos críticos com a imagem que obtemos em na borda da região, vemos que
O ponto máximo é o ponto que está na borda da região e os pontos mínimos, são os pontos , , e em que a imagem é .
Finalmente chegamos ao fim!!
E todos viveram felizes para sempre! 😉 Entendeu tudo? Responde Aí

Resposta
a) , , , , e
b)
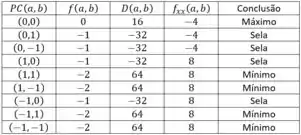
c) Ponto máximo contido em , cuja imagem é .
Ponto mínimo em , , e em que a imagem é .