UFABC. Cálculo. Funções de Várias Variáveis. Lista 5 - Pontos Críticos, Máximos e Mínimos, Multiplicadores de Lagrange. Questão 2a.
2 - Encontre o máximo e mínimo globais de cada uma das seguintes funções:
a) , , ;
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nessa questão foi dada uma função e devemos calcular seus pontos de máximos e mínimos dentro da região delimitada por e .
Mas e aí? Como vamos descobrir os pontos de máximos e mínimos se considerarmos apenas a função dentro da área delimitada??
Veja só! Se encontrarmos os pontos críticos de , podemos ignorar os pontos que estiverem fora da região. Não é?
A diferença é que nas bordas da região, talvez o ponto de máximo ou mínimo não seja um ponto crítico, então temos que usar um método diferente para esses casos. Perceba que a questão apenas nos pediu um máximo global e um mínimo global. Ou seja, queremos calcular (dentro da região) o ponto em que o valor de é máximo e o ponto onde o valor de é mínimo.
Mas vamos com calma, uma coisa de cada vez, primeiro vamos usar o método que já conhecemos.
Bora lá! 🐱👤
Passo 2
O método comum, é de calcular e e igualar a , assim obtendo um sistema. As possíveis soluções desse sistema, serão os candidatos para máximos ou mínimos de .
Vamos obter
Como se torna uma constante quando derivamos em relação a , a derivada de é .
Vamos calcular , agora é a vez de se comportar como uma constante, logo a derivada de
Igualando a , vamos obter um sistema
Vamos analisar a primeira equação.
Calculando o dos dois lados, temos
Agora analisando a segunda equação.
Calculando o dos dois lados da equação, temos
Com isso, podemos concluir que
é igual a ! Isso vai nos ajudar.
Passo 3
Também podemos escrever o sistema como
Vamos pensar! Qual o valor podemos colocar no para que este valor mais ele mesmo dê o mesmo resultado só que negativo?
O e o !
Ou seja, , onde é uma constante inteira.
Com isso, descobrimos que os pontos para , , ...
São pontos críticos.
Porém estamos limitados pela nossa região, então apenas nos interessa o ponto já que a partir de , o ponto está fora da região.
Agora temos que olhar para as bordas da região
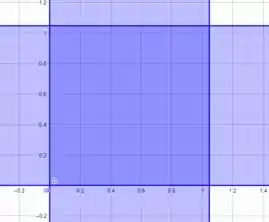
Pra isso, vamos ver o comportamento da função quando , , e .
Substituindo em temos.
Obtemos uma função de amplitude .
Dentro do intervalo , a função só cresce, logo, o ponto entra para a nossa lista!
Continuando com as substituições, vamos ver para
Como a função só cresce, entre e , os pontos e entram para nossa lista de suspeitos.
Entendeu?
Passo 4
Agora, faremos o mesmo para as bordas perpendiculares ao eixo .
Para , temos
Seguindo a mesma ideia do passo anterior, teríamos o ponto mas observe que ele é o mesmo ponto .
Por fim, para , temos
Não temos mais pontos para adicionar à nossa lista, já que os vértices do lado já estão sob suspeitas.
Por último, a gente calcula o valor de nos pontos encontrados e comparamos os resultados para ver qual é o máximo e qual é o mínimo.
Entendido?
Passo 5
Para o ponto , temos
Para o ponto
Para o ponto
Organizando um pouquinho mais, temos
Para o ponto
Encontramos o valor de cada ponto, agora vamos compara-los
Passo 6
Comparando os valores de para cada ponto, vemos que o menor ponto é o ponto , onde a função resultou em .
Já o maior resultado, foi obtido pelo ponto , onde a função vale .
Ou seja, nosso mínimo global dentro da região limitada é o ponto . Já o máximo global dentro da região limitada é o ponto .
Podemos conferir, observando o pedaço da função que está contida no intervalo.
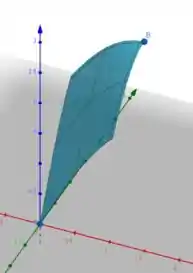
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
Mínimo global: , .
Máximo global: , .