Seja definida na região triangular fechada com vértices e . Qual das afirmativas abaixo é verdadeira?
- O máximo absoluto de em é e o mínimo absoluto de em é
- O máximo absoluto de em é e o mínimo absoluto de em é
- O máximo absoluto de em é e o mínimo absoluto de em é
- O máximo absoluto de em é e o mínimo absoluto de em é
- Não sei
Passo 1
Vamos começar visualizando o conjunto . Marcando os pontos, temos:
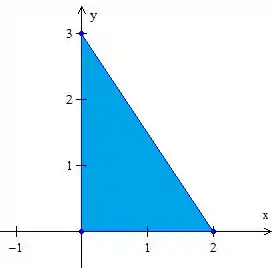
Então o problema consiste em procurar máximos e mínimos globais dentro dessa região fechada e limitada.
Passo 2
Vamos achar os pontos críticos da função, igualando as derivadas parciais a zero:
Temos
Ou seja, a função não tem pontos críticos. Logo, os máximos e mínimos globais só podem estar na fronteira dessa região.
Passo 3
Analisando a fronteira, temos de encontrar a equação da reta que une os pontos e . A equação é:
Substituindo o ponto :
No ponto :
Então:
Para
Passo 4
Então temos os lados:
Lados em que são os lados do triângulo.
Vamos verificar se há máximos e mínimos da função sobre esses lados, não esquecendo que os vértices também são candidatos a valores extremos.
Passo 5
Comecemos pelo lado . Lembrando a nossa função:
E o primeiro lado:
Substituindo o lado na função:
Derivando temos:
Logo não há pontos candidatos a máximos e mínimos em .
Passo 6
Lado : Lembrando a nossa função:
O lado é :
Substituindo o lado na função:
Derivando temos:
Logo não há pontos candidatos a máximos e mínimos em .
Passo 7
Lado : Lembrando a nossa função:
Temos:
Substituindo o lado na função:
Derivando temos:
Logo não há pontos candidatos a máximos e mínimos em .
Passo 8
Então só temos os vértices da região como candidatos. Testando seus valores, temos:
Logo o máximo absoluto de em é e o mínimo absoluto de em é .
Resposta
c) O máximo absoluto de em é e o mínimo absoluto de em é