Os valores máximo e mínimo absolutos de
Na região
São, respectivamente:
Passo 1
Para encontrar os pontos de máximo e mínimo globais de uma função com restrição o processo é sempre o mesmo: Verificar se há um ponto crítico dentro da região, e verificar se há máximos e mínimos na fronteira da região.
Verificando pontos críticos dentro da região:
EITA, não pode né?
Isso significa que a função não tem pontos críticos dentro da região.
Passo 2
Vamos agora pegar os vértices da nossa região.
Primeiro vamos entender qual é essa região. Plotando as retas do conjunto, temos
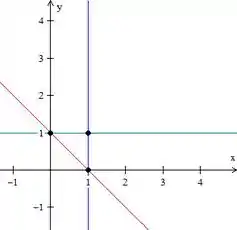
Mas, como na verdade não temos igualdades e sim desigualdades, nossa região corresponde a área interior desse triangulo aí.
E os pontos dos vértices são esses pontos marcados:
Portanto, temos 3 pontos candidatos a máximo e mínimo.
Passo 3
Agora, devemos verificar pontos de máximo ou mínimo na fronteira.
Assim, temos 3 lados a serem verificados:
Quando em que são os lados do triangulo.
Em cada lado a função só depende de uma variável, e nós temos que achar os pontos críticos dessas 3 “subfunções”.
Passo 4
Comecemos pelo lado . Lembrando a nossa função:
E o primeiro lado:
Substituindo o lado na função:
Temos que achar o valor de máximo dessa função, vamos derivar e igualar a zero. Neste caso derivamos em relação a
De novo, não pode isso, então não temos pontos críticos nesse lado.
Passo 5
Agora precisamos fazer o mesmo pro segundo lado :
Substituindo esse lado na função, teremos:
Temos que achar os pontos críticos dessa função, vamos derivar e igualar a zero. Neste caso derivamos em relação a
Então temos o ponto
Mas esse nós já separamos quando pegamos os vértices do triangulo, então não acrescentou nada de novo.
Passo 6
Vamos verificar para o terceiro lado :
Substituindo-o na função:
Desenvolvendo,
Neste caso derivamos em relação a
Isso também é impossível, logo, não temos candidatos sobre esse lado também.
Passo 7
Ok, agora já temos todo o material necessário para terminar de vez com isso e dizer quais são os pontos de máximo e mínimo!
Os nossos candidatos são os pontos:
Passo 8
Só nos resta calcular o valor da função em cada ponto. Lembrando que
Então temos
Show, então o valor mínimo global é 0 e o valor máximo global é .